
【题目】已知椭圆![]() 的中心在原点,左焦点
的中心在原点,左焦点![]() 、右焦点
、右焦点![]() 都在
都在![]() 轴上,点
轴上,点![]() 是椭圆
是椭圆![]() 上的动点,
上的动点,![]() 的面积的最大值为
的面积的最大值为![]() ,在
,在![]() 轴上方使
轴上方使![]() 成立的点
成立的点![]() 只有一个.
只有一个.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的两直线
的两直线![]() ,
,![]() 分别与椭圆
分别与椭圆![]() 交于点
交于点![]() ,
,![]() 和点
和点![]() ,
,![]() ,且
,且![]() ,比较
,比较![]() 与
与![]() 的大小.
的大小.
科目:高中数学 来源: 题型:
【题目】《九章算术》中将底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵”;底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”;四个面均为直角三角形的四面体称为“鳖膈”.如图在堑堵ABC-A1B1C1中,AC⊥BC,且AA1=AB=2.下列说法正确的是( )
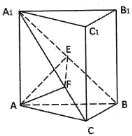
A.四棱锥B-A1ACC1为“阳马”
B.四面体A1C1CB为“鳖膈”
C.四棱锥B-A1ACC1体积最大为![]()
D.过A点分别作AE⊥A1B于点E,AF⊥A1C于点F,则EF⊥A1B
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张师傅欲将一球形的石材工件削砍加工成一圆柱形的新工件,已知原球形工件的半径为![]() ,则张师傅的材料利用率的最大值等于(注:材料利用率=
,则张师傅的材料利用率的最大值等于(注:材料利用率=![]() )( )
)( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】设球半径为R,圆柱的体积为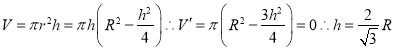 时圆柱的体积最大为
时圆柱的体积最大为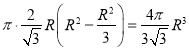 ,因此材料利用率=
,因此材料利用率=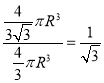 ,选C.
,选C.
点睛:空间几何体与球接、切问题的求解方法
求解球与棱柱、棱锥的接、切问题时,一般过球心及接、切点作截面,把空间问题转化为平面图形与圆的接、切问题,再利用平面几何知识寻找几何中元素间的关系求解.
【题型】单选题
【结束】
12
【题目】已知抛物线![]() :
: ![]()
![]() 在点
在点![]() 处的切线与曲线
处的切线与曲线![]() :
: ![]() 相切,若动直线
相切,若动直线![]() 分别与曲线
分别与曲线![]() 、
、![]() 相交于
相交于![]() 、
、![]() 两点,则
两点,则![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一,为坚决打赢脱贫攻坚战,某帮扶单位考察了甲乙两种不同的农产品加工生产方式,现对两种生产方式加工的产品质量进行测试并打分对比,得到如下数据:
生产方式甲 | 分值区间 |
|
|
|
|
|
频数 | 20 | 30 | 100 | 40 | 10 | |
生产方式乙 | 分值区间 |
|
|
|
|
|
频数 | 25 | 35 | 50 | 30 |
其中产品质量按测试指标可划分为:指标在区间![]() 上的为特优品,指标在区间
上的为特优品,指标在区间![]() 上的为一等品,指标在区间
上的为一等品,指标在区间![]() 上的为二等品.
上的为二等品.
(1)用事件![]() 表示“按照生产方式甲生产的产品为特优品”,估计
表示“按照生产方式甲生产的产品为特优品”,估计![]() 的概率;
的概率;
(2)填写下面列联表,并根据列联表判断能否有![]() 的把握认为“特优品”与生产方式有关?
的把握认为“特优品”与生产方式有关?
特优品 | 非特优品 | |
生产方式甲 | ||
生产方式乙 |
(3)根据打分结果对甲乙两种生产方式进行优劣比较.
附表:
| 0.10 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
参考公式: ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知圆![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() ,动圆
,动圆![]() 与圆
与圆![]() 内切且与圆
内切且与圆![]() 外切.
外切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知![]() 与
与![]() 为平面内的两个定点,过
为平面内的两个定点,过![]() 点的直线
点的直线![]() 与轨迹
与轨迹![]() 交于
交于![]() ,
,![]() 两点,求四边形
两点,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,抛物线C:
,抛物线C:![]() 的焦点到直线l:
的焦点到直线l:![]() 的距离为
的距离为![]() .
.
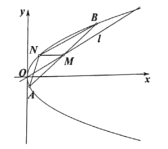
(1)求m的值.
(2)如图,已知抛物线C的动弦![]() 的中点M在直线l上,过点M且平行于x轴的直线与抛物线C相交于点N,求
的中点M在直线l上,过点M且平行于x轴的直线与抛物线C相交于点N,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为广泛开展垃圾分类的宣传教育和倡导工作,使市民树立垃圾分类的环保意识,学会垃圾分类的知识,特举办了“垃圾分类知识竞赛".据统计,在为期1个月的活动中,共有两万人次参与网络答题.市文明实践中心随机抽取100名参与该活动的市民,以他们单次答题得分作为样本进行分析,由此得到如图所示的频率分布直方图:

(1)求图中a的值及参与该活动的市民单次挑战得分的平均成绩![]() (同一组中数据用该组区间中点值作代表);
(同一组中数据用该组区间中点值作代表);
(2)若垃圾分类答题挑战赛得分落在区间![]() 之外,则可获得一等奖奖励,其中
之外,则可获得一等奖奖励,其中![]() ,s分别为样本平均数和样本标准差,计算可得
,s分别为样本平均数和样本标准差,计算可得![]() ,若某人的答题得分为96分,试判断此人是否获得一等奖;
,若某人的答题得分为96分,试判断此人是否获得一等奖;
(3)为扩大本次“垃圾分类知识竞赛”活动的影响力,市文明实践中心再次组织市民组队参场有奖知识竞赛,竞赛共分五轮进行,已知“光速队”与“超能队”五轮的成绩如下表:
成绩 | 第一轮 | 第二轮 | 第三轮 | 第四轮 | 第五轮 |
“光速队” | 93 | 98 | 94 | 95 | 90 |
“超能队” | 93 | 96 | 97 | 94 | 90 |
①分别求“光速队”与“超能队”五轮成绩的平均数和方差;
②以上述数据为依据,你认为"光速队”与“超能队”的现场有奖知识竞赛成绩谁更稳定?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com