
【题目】已知a∈R,当x>0时,f(x)=log2( ![]() +a).
+a).
(1)若函数f(x)过点(1,1),求此时函数f(x)的解析式;
(2)若函数g(x)=f(x)+2log2x只有一个零点,求实数a的范围;
(3)设a>0,若对任意实数t∈[ ![]() ,1],函数f(x)在[t,t+1]上的最大值与最小值的差不大于1,求实数a的取值范围.
,1],函数f(x)在[t,t+1]上的最大值与最小值的差不大于1,求实数a的取值范围.
【答案】
(1)解:∵a∈R,当x>0时,f(x)=log2( ![]() +a).
+a).
函数f(x)过点(1,1),
∴f(1)=log2(1+a)=1,解得a=1,
∴此时函数f(x)=log2( ![]() +1)(x>0).
+1)(x>0).
(2)解:g(x)=f(x)+2log2x= ![]() +2log2x=log2(x+ax2),
+2log2x=log2(x+ax2),
∵函数g(x)=f(x)+2log2x只有一个零点,
∴g(x)=f(x)+2log2x=log2(x+ax2)=0
∴( ![]() +a)x2=1化为ax2+x﹣1=0
+a)x2=1化为ax2+x﹣1=0
∴h(x)=ax2+x=1在(0,+∞)上只有一个解,
∴当a=0时,h(x)=x﹣1,只有一个零点,可得x=1;
当a≠0时,h(x)=ax2+x﹣1在(0,+∞)上只有一个零点,
当a>0时,成立;
当a<0时,令△=1+4a=0解得a=﹣ ![]() ,可得x=2.
,可得x=2.
综上可得,a≥0或a=﹣ ![]() .
.
(3)解:f(x)= ![]() ,
,
f′(x)=﹣ ![]() ,
,
当x>0时,f′(x)<0,f(x)在[t,t+1]上的最大值与最小值分别是f(t)与f(t+1),
由题意,得f(t)﹣f(t+1)≤1,
∴ ![]() ≤2,
≤2,
整理,得a≥ ![]() ,
,
设Q(t)= ![]() ,
,
Q′(t)= ![]() ,
,
当t∈[ ![]() ,1]时,Q′(t)<0,
,1]时,Q′(t)<0,
则a≥Q(t),∴a≥Q( ![]() ),解得a≥
),解得a≥ ![]() .
.
∴实数a的取值范围是[ ![]() ,+∞).
,+∞).
【解析】(1)由f(1)=log2(1+a)=1,解得a=1,由此能求出此时函数f(x)的解析式.(2)g(x)=log2(x+ax2),由函数g(x)只有一个零点,从而h(x)=ax2+x=1在(0,+∞)上只有一个解,由此能求出a.(3)f(x)= ![]() ,
, ![]() ,由题意,得f(t)﹣f(t+1)≤1,从而a≥
,由题意,得f(t)﹣f(t+1)≤1,从而a≥ ![]() ,设Q(t)=
,设Q(t)= ![]() ,Q′(t)=
,Q′(t)= ![]() ,由此利用导数性质能求出实数a的取值范围.
,由此利用导数性质能求出实数a的取值范围.


科目:高中数学 来源: 题型:
【题目】如图,关于正方体ABCD﹣A1B1C1D1 , 下面结论错误的是( ) 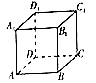
A.BD⊥平面ACC1A1
B.AC⊥BD
C.A1B∥平面CDD1C1
D.该正方体的外接球和内接球的半径之比为2:1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.命题“若x≠2或y≠7,则x+y≠9”的逆命题为真命题
B.命题“若x2=4,则x=2”的否命题是“若x2=4,则x≠2”
C.命题“若x2<1,则﹣1<x<1”的逆否命题是“若x<﹣1或x>1,则x2>1”
D.若命题p:x∈R,x2﹣x+1>0,q:x0∈(0,+∞),sinx0>1,则(¬p)∨q为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|ax﹣x2|+2b(a,b∈R).
(1)当a=﹣2,b=﹣ ![]() 时,解方程f(2x)=0;
时,解方程f(2x)=0;
(2)当b=0时,若不等式f(x)≤2x在x∈[0,2]上恒成立,求实数a的取值范围;
(3)若a为常数,且函数f(x)在区间[0,2]上存在零点,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x|x﹣a|+2x.
(1)若函数f(x)在R上是增函数,求实数a的取值范围;
(2)求所有的实数a,使得对任意x∈[1,2]时,函数f(x)的图象恒在函数g(x)=2x+1图象的下方;
(3)若存在a∈[﹣4,4],使得关于x的方程f(x)=tf(a)有三个不相等的实数根,求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com