
【题目】已知函数![]() .
.
(1)求![]() 单调区间与极值;
单调区间与极值;
(2)当函数![]() 有两个极值点时,求实数
有两个极值点时,求实数![]() 的取值范围.
的取值范围.
【答案】(1)单调递增区间为![]() ;单调递减区间为
;单调递减区间为![]() ;
;![]() 极小值为
极小值为![]() ,不存在极大值;
,不存在极大值;
(2)![]()
【解析】
(1)首先求出函数的定义域、导函数,即可求出函数的单调区间与极值;
(2)首先求出导函数![]() ,由函数
,由函数![]() 有两个极值点,即等价于
有两个极值点,即等价于![]() 有两个解,即
有两个解,即![]() 有两个解,即求
有两个解,即求![]() 有两个解,结合(1)即可求出参数的取值范围;
有两个解,结合(1)即可求出参数的取值范围;
解:(1)依题意可知函数![]() 的定义域为
的定义域为![]()
![]()
当![]() 时,
时,![]() ,故函数
,故函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,故函数
,故函数![]() 在
在![]() 上单调递减;
上单调递减;
故函数![]() 在
在![]() 时取得极小值,即
时取得极小值,即![]() ,不存在极大值;
,不存在极大值;
综上所述,单调递增区间为![]() ;单调递减区间为
;单调递减区间为![]() ;
;![]() 极小值为
极小值为![]() ,不存在极大值;
,不存在极大值;
(2)因为![]() ,
,
所以![]()
求函数![]() 有两个极值点,又因为函数
有两个极值点,又因为函数![]() 是连续函数,等价于
是连续函数,等价于![]() 有两个解,即
有两个解,即![]() 有两个解,
有两个解,
由(1),可得求![]() 有两个解,即求
有两个解,即求![]() 有两个解,
有两个解,
又因为![]() ,且函数
,且函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
所以![]()
即![]()


科目:高中数学 来源: 题型:
【题目】某市大力推广纯电动汽车,对购买用户依照车辆出厂续驶里程R的行业标准,予以地方财政补贴.其补贴标准如下表:
出厂续驶里程R(公里) | 补贴(万元/辆) |
| 3 |
| 4 |
| 4.5 |
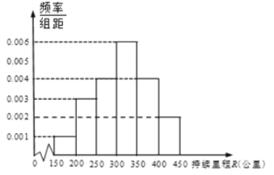
2019年底随机调查该市1000辆纯电动汽车,统计其出厂续驶里程R,得到频率分布直方图如上图所示用样本估计总体,频率估计概率,解决如下问题:
(1)求该市每辆纯电动汽车2019年地方财政补贴的均值;
(2)某企业统计2019年其充电站100天中各天充电车辆数,得如下的频数分布表:
辆数 |
|
|
|
|
天数 | 20 | 30 | 40 | 10 |
(同一组数据用该区间的中点值作代表)
2020年3月,国家出台政策,将纯电动汽车财政补贴逐步转移到充电基础设施建设上来该企业拟将转移补贴资金用于添置新型充电设备,现有直流、交流两种充电桩可供购置.直流充电桩5万元/台,每台每天最多可以充电30辆车,每天维护费用500元/台;交流充电桩1万元/台,每台每天最多可以充电4辆车,每天维护费用80元/台.该企业现有两种购置方案:
方案一:购买100台直流充电桩和900台交流充电桩;
方案二:购买200台直流充电桩和400台交流充电桩.
假设车辆充电时优先使用新设备,且充电一辆车产生25元的收入,用2019年的统计数据,分别估计该企业在两种方案下新设备产生的最大日利润.(日利润![]() 日收入
日收入![]() 日维护费用).
日维护费用).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 平面ABCD,
平面ABCD,![]() ,E为PD的中点,F在AD上且
,E为PD的中点,F在AD上且![]() .
.
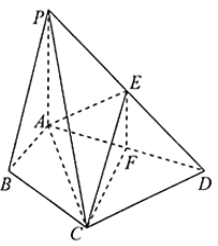
(1)求证:CE//平面PAB;
(2)若PA=2AB=2,求四面体PACE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】冠状病毒是一个大型病毒家族,己知可引起感冒以及中东呼吸综合征(![]() )和严重急性呼吸综合征(
)和严重急性呼吸综合征(![]() )等较严重疾病.而今年出现在湖北武汉的新型冠状病毒(
)等较严重疾病.而今年出现在湖北武汉的新型冠状病毒(![]() )是以前从未在人体中发现的冠状病毒新毒株.人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等.在较严重病例中,感染可导致肺炎、严重急性呼吸综合征、肾衰竭,甚至死亡.
)是以前从未在人体中发现的冠状病毒新毒株.人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等.在较严重病例中,感染可导致肺炎、严重急性呼吸综合征、肾衰竭,甚至死亡.
某医院为筛查冠状病毒,需要检验血液是否为阳性,现有n(![]() )份血液样本,有以下两种检验方式:
)份血液样本,有以下两种检验方式:
方式一:逐份检验,则需要检验n次.
方式二:混合检验,将其中k(![]() 且
且![]() )份血液样本分别取样混合在一起检验.
)份血液样本分别取样混合在一起检验.
若检验结果为阴性,这k份的血液全为阴性,因而这k份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这k份血液究竟哪几份为阳性,就要对这k份再逐份检验,此时这k份血液的检验次数总共为![]() .
.
假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为p(![]() ).现取其中k(
).现取其中k(![]() 且
且![]() )份血液样本,记采用逐份检验方式,样本需要检验的总次数为
)份血液样本,记采用逐份检验方式,样本需要检验的总次数为![]() ,采用混合检验方式,样本需要检验的总次数为
,采用混合检验方式,样本需要检验的总次数为![]() .
.
(1)若![]() ,试求p关于k的函数关系式
,试求p关于k的函数关系式![]() ;
;
(2)若p与干扰素计量![]() 相关,其中
相关,其中![]() (
(![]() )是不同的正实数,
)是不同的正实数,
满足![]() 且
且![]() (
(![]() )都有
)都有![]() 成立.
成立.
(i)求证:数列![]() 等比数列;
等比数列;
(ii)当![]() 时,采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数的期望值更少,求k的最大值
时,采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数的期望值更少,求k的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网店统计了连续三天售出商品的种类情况:第一天售出19种商品,第二天售出13种商品,第三天售出18种商品;前两天都售出的商品有3种,后两天都售出的商品有4种,则该网店
①第一天售出但第二天未售出的商品有______种;
②这三天售出的商品最少有_______种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】埃及金字塔是古埃及的帝王(法老)陵墓,世界七大奇迹之一,其中较为著名的是胡夫金字塔.令人吃惊的并不仅仅是胡夫金字塔的雄壮身姿,还有发生在胡夫金字塔上的数字“巧合”.如胡夫金字塔的底部周长如果除以其高度的两倍,得到的商为3.14159,这就是圆周率较为精确的近似值.金字塔底部形为正方形,整个塔形为正四棱锥,经古代能工巧匠建设完成后,底座边长大约230米.因年久风化,顶端剥落10米,则胡夫金字塔现高大约为( )
A.128.5米B.132.5米C.136.5米D.110.5米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为平面直角坐标系xOy中的点集,从
为平面直角坐标系xOy中的点集,从![]() 中的任意一点P作x轴、y轴的垂线,垂足分别为M,N,记点M的横坐标的最大值与最小值之差为x(
中的任意一点P作x轴、y轴的垂线,垂足分别为M,N,记点M的横坐标的最大值与最小值之差为x(![]() ),点N的纵坐标的最大值与最小值之差为y(
),点N的纵坐标的最大值与最小值之差为y(![]() ).若
).若![]() 是边长为1的正方形,给出下列三个结论:
是边长为1的正方形,给出下列三个结论:
①x(Q)的最大值为![]()
②x(Q)+y(Q)的取值范围是![]()
③x(Q)-y(Q)恒等于0.
其中所有正确结论的序号是_________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() ,Q为l上的动点,以OQ为边作等边三角形OPQ,且三点O,P,Q按逆时针方向排列.
,Q为l上的动点,以OQ为边作等边三角形OPQ,且三点O,P,Q按逆时针方向排列.
(Ⅰ)设点P运动轨迹E的直角坐标方程;
(Ⅱ)若曲线![]() 经过伸缩变换
经过伸缩变换![]() 得到曲线
得到曲线![]() ,若点M为曲线
,若点M为曲线![]() 上的动点,且点M到曲线E的最小距离为1,求实数a的值.
上的动点,且点M到曲线E的最小距离为1,求实数a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com