
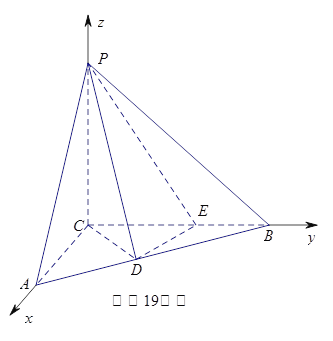
【题目】如图,三棱锥![]() 中,
中,![]() 平面
平面

![]() ,
,![]() ,
,![]() 。
。![]() 分别为线段
分别为线段![]() 上的点,且
上的点,且![]() 。
。
(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值。
的余弦值。
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)要证线面垂直,就是要证线线垂直,题中由![]() 平面
平面![]() ,可知
,可知![]() ,再分析已知由
,再分析已知由![]() 得
得![]() ,这样与
,这样与![]() 垂直的两条直线都已找到,从而可得线面垂直;(2)求二面角的大小,可心根据定义作出二面角的平面角,求出这个平面角的大小,本题中,由于
垂直的两条直线都已找到,从而可得线面垂直;(2)求二面角的大小,可心根据定义作出二面角的平面角,求出这个平面角的大小,本题中,由于![]() ,
,![]() 平面
平面![]() ,因此
,因此![]() 两两垂直,可以他们为
两两垂直,可以他们为![]() 轴建立空间直角坐标系,写出图中各点的坐标,求出平面
轴建立空间直角坐标系,写出图中各点的坐标,求出平面![]() 和平面
和平面![]() 的法向量
的法向量![]() ,向量
,向量![]() 的夹角与二面角相等或互补,由此可得结论.
的夹角与二面角相等或互补,由此可得结论.
试题解析:(1)证明:由PC![]() 平面ABC,DE
平面ABC,DE![]() 平面ABC,故PC
平面ABC,故PC![]() DE
DE
由CE=2,CD=DE=![]() 得
得![]() CDE为等腰直角三角形,故CD
CDE为等腰直角三角形,故CD![]() DE
DE
由PC![]() CD=C,DE垂直于平面PCD内两条相交直线,故DE
CD=C,DE垂直于平面PCD内两条相交直线,故DE![]() 平面PCD
平面PCD
(2)解:由(1)知,![]() CDE为等腰直角三角形,
CDE为等腰直角三角形,![]() DCE=
DCE=![]() ,如(19)图,过点D作DF垂直CE于F,易知DF=FC=EF=1,又已知EB=1,
,如(19)图,过点D作DF垂直CE于F,易知DF=FC=EF=1,又已知EB=1,
故FB=2.
由![]() ACB=
ACB=![]() 得DF
得DF![]() AC,
AC,![]() ,故AC=
,故AC=![]() DF=
DF=![]() .
.
以C为坐标原点,分别以![]() 的方程为x轴,y轴,z轴的正方向建立空间直角坐标系,则C(0,0,0,),P(0,0,3),A(
的方程为x轴,y轴,z轴的正方向建立空间直角坐标系,则C(0,0,0,),P(0,0,3),A(![]() ,0,0),E(0,2,0),D(1,1,0),
,0,0),E(0,2,0),D(1,1,0),![]()
![]()
设平面![]() 的法向量
的法向量![]() ,
,
由![]() ,
,![]() ,
,
得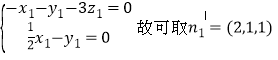 .
.
由(1)可知DE![]() 平面PCD,故平面PCD的法向量
平面PCD,故平面PCD的法向量![]() 可取为
可取为![]() ,即
,即![]() .
.
从而法向量![]() ,
,![]() 的夹角的余弦值为
的夹角的余弦值为 ,
,
故所求二面角A-PD-C的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】小明一家订阅的晚报会在下午5:30~6:30之间的任何一个时间随机地被送到,小明一家人在下午6:00~7:00之间的任何一个时间随机地开始晚餐.
(1)你认为晚报在晚餐开始之前被送到和晚餐开始之后被送到哪一种可能性更大?
(2)晚报在晚餐开始之前被送到的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M={(x,y)|y=f(x)},若对于任意实数对(x1,y1)∈M,存在(x2,y2)∈M,使x1x2+y1y2=0成立,则称集合M具有∟性,给出下列四个集合:
①M={(x,y)|y=x3﹣2x2+3}; ②M={(x,y)|y=log2(2﹣x)};
③M={(x,y)|y=2﹣2x}; ④M={(x,y)|y=1﹣sinx};
其中具有∟性的集合的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,直线y=
,直线y= ![]() x为曲线y=f(x)的切线(e为自然对数的底数).
x为曲线y=f(x)的切线(e为自然对数的底数).
(1)求实数a的值;
(2)用min{m,n}表示m,n中的最小值,设函数g(x)=min{f(x),x﹣ ![]() }(x>0),若函数h(x)=g(x)﹣cx2为增函数,求实数c的取值范围.
}(x>0),若函数h(x)=g(x)﹣cx2为增函数,求实数c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() (
(![]() ,且
,且![]() ,
,![]() )是定义在区间
)是定义在区间![]() 上的奇函数,
上的奇函数,
(1)求![]() 的值和实数
的值和实数![]() 的值;
的值;
(2)判断函数![]() 在区间
在区间![]() 上的单调性,并说明理由;
上的单调性,并说明理由;
(3)若![]() 且
且![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的右焦点为F,上顶点为A,短轴长为2,O为原点,直线AF与椭圆C的另一个交点为B,且△AOF的面积是△BOF的面积的3倍.
=1(a>b>0)的右焦点为F,上顶点为A,短轴长为2,O为原点,直线AF与椭圆C的另一个交点为B,且△AOF的面积是△BOF的面积的3倍. 
(1)求椭圆C的方程;
(2)如图,直线l:y=kx+m与椭圆C相交于P,Q两点,若在椭圆C上存在点R,使OPRQ为平行四边形,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com