
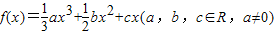 的图象在点(x,f(x))处的切线的斜率为k(x),且函数
的图象在点(x,f(x))处的切线的斜率为k(x),且函数 为偶函数.若函数k(x)满足下列条件:①k(-1)=0;②对一切实数x,不等式
为偶函数.若函数k(x)满足下列条件:①k(-1)=0;②对一切实数x,不等式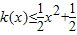 恒成立.
恒成立.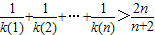 (n∈N*).
(n∈N*).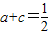 ,再由
,再由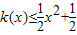 对一切实数x恒成立,解得a、c的值,即得函数k(x)的表达式.
对一切实数x恒成立,解得a、c的值,即得函数k(x)的表达式.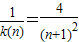 ,即证
,即证 ,把
,把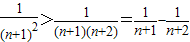 代入要证不等式的左边化简即可证得不等式成立.
代入要证不等式的左边化简即可证得不等式成立. 为偶函数,得
为偶函数,得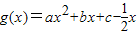 为偶函数,显然有
为偶函数,显然有 .…(2分)
.…(2分)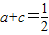 .…(3分)
.…(3分)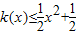 对一切实数x恒成立,
对一切实数x恒成立, 恒成立.…(4分)
恒成立.…(4分) 时,不符合题意.…(5分)
时,不符合题意.…(5分)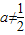 时,应满足
时,应满足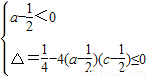 ,
,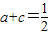 ,解得
,解得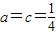 .…(7分) 所以
.…(7分) 所以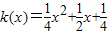 . …(8分)
. …(8分) ,所以
,所以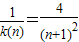 .…(9分)
.…(9分) 成立,
成立,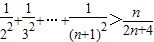 .…(10分)
.…(10分)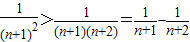 ,…(12分)
,…(12分)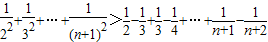 =
=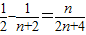 .
. 成立.…(14分)
成立.…(14分)

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
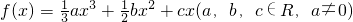 的图象在点(x,f(x))处的切线的斜率为k(x),且函数
的图象在点(x,f(x))处的切线的斜率为k(x),且函数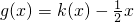 为偶函数.若函数k(x)满足下列条件:①k(-1)=0;②对一切实数x,不等式
为偶函数.若函数k(x)满足下列条件:①k(-1)=0;②对一切实数x,不等式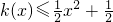 恒成立.
恒成立. (n∈N*).
(n∈N*).查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省实验中学高三(上)第二次考试数学试卷(文科)(解析版) 题型:解答题
 的图象在点(x,f(x))处的切线的斜率为k(x),且函数
的图象在点(x,f(x))处的切线的斜率为k(x),且函数 为偶函数.若函数k(x)满足下列条件:①k(-1)=0;②对一切实数x,不等式
为偶函数.若函数k(x)满足下列条件:①k(-1)=0;②对一切实数x,不等式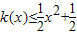 恒成立.
恒成立.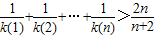 (n∈N*).
(n∈N*).查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省安庆市望江中学高三(上)第五次月考数学试卷(理科)(解析版) 题型:解答题
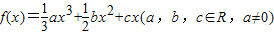 的图象在点(x,f(x))处的切线的斜率为k(x),且函数
的图象在点(x,f(x))处的切线的斜率为k(x),且函数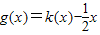 为偶函数.若函数k(x)满足下列条件:①k(-1)=0;②对一切实数x,不等式
为偶函数.若函数k(x)满足下列条件:①k(-1)=0;②对一切实数x,不等式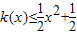 恒成立.
恒成立. (n∈N*).
(n∈N*).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com