
已知集合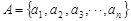 ,其中
,其中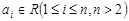 ,
,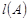 表示
表示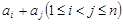 的所有不同值的个数.
的所有不同值的个数.
(1)已知集合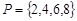 ,
,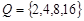 ,分别求
,分别求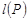 ,
,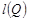 ;
;
(2)求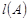 的最小值.
的最小值.
(1)l(P)=5 ,l(Q)=6
(2)对这样的集合A,l(A)=2n-3,所以l(A)的最小值为2n-3.
解析试题分析:(1)由2+4=6,2+6=8,2+8=10,4+6=10,4+8=12,6+8=14,
得l(P)=5
由2+4=6,2+8=10,2+16=18,4+8=12,4+16=20,8+16=24,
得l(Q)=6
(2)不妨设a1<a2<a3<…<an,可得
a1+a2<a1+a3<…<a1+an<a2+an<a3+an<…<an-1+an,
故ai+aj (1≤i<j≤n)中至少有2n-3个不同的数,即l(A)≥2n-3.
事实上,设a1,a2,a3,…,an成等差数列,考虑ai+aj (1≤i<j≤n),根据等差数列的性质,当i+j≤n时, ai+aj=a1+ai+j-1;当i+j>n时, ai+aj=ai+j-n+an;
因此每个和ai+aj(1≤i<j≤n)等于a1+ak(2≤k≤n)中的一个,或者等于al+an(2≤l≤n-1)中的一个.故对这样的集合A,l(A)=2n-3,所以l(A)的最小值为2n-3.
考点:本题主要考查集合的意义,等差数列的性质。
点评:新定义问题,利用新定义集合确定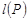 ,
,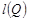 属于简单问题。而求
属于简单问题。而求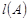 的最小值的方法,则具有一定难度,特别是假设“排序”难以想到,这是解决问题的关键所在。
的最小值的方法,则具有一定难度,特别是假设“排序”难以想到,这是解决问题的关键所在。


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
已知集合A=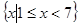 ,B={x|2<x<10},C={x|x<a},全集为实数集R.
,B={x|2<x<10},C={x|x<a},全集为实数集R.
(Ⅰ)求A∪B,(CRA)∩B;
(Ⅱ)如果A∩C≠φ,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知集合A={a2,a+1,-3},B={a-3,a2+1,2a-1},若A∩B={-3},
(Ⅰ)求实数a的值.
(Ⅱ)设 ,求不等式
,求不等式 的解集。
的解集。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com