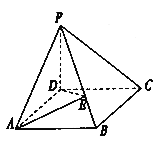
【题目】如图在棱锥
中， 
为矩形， 
面
， 
， 
与面
成
角， 
与面
成
角.
（1）在
上是否存在一点
，使
面
，若存在确定
点位置，若不存在，请说明理由；
（2）当
为
中点时，求二面角
的余弦值.
【答案】（1）见解析（2）
【解析】试题分析：（1）法一：要证明PC⊥面ADE，只需证明AD⊥PC，通过证明
即可，然后推出存在点E为PC中点．
法二：建立如图所示的空间直角坐标系D﹣XYZ，设
，通过
得到
，即存在点E为PC中点．
（2）由（1）知求出面ADE的法向量，面PAE的法向量，利用空间向量的数量积．求解二面角P﹣AE﹣D的余弦值．
试题解析：
（Ⅰ）法一：要证明PC⊥面ADE，易知AD⊥面PDC，即得AD⊥PC，故只需
即可，所以由
,即存在点E为PC中点
法二：建立如图所示的空间直角坐标系D－XYZ，
由题意知PD＝CD＝1，
，设
， 
，
,
由
，得
，
即存在点E为PC中点。
（Ⅱ）由（Ⅰ）知
， 
， 
， 
， 
， 
， 
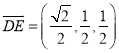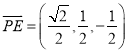
设面ADE的法向量为
，面PAE的法向量为
由的法向量为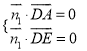
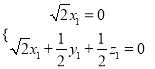得， 
得
同理求得
所以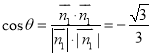
故所求二面角P－AE－D的余弦值为
.
期末冲刺100分创新金卷完全试卷系列答案科目：高中数学 来源： 题型：
【题目】有甲乙两家公司都愿意聘用某求职者，这两家公式的具体聘用信息如下：
（1）根据以上信息，如果你是该求职者，你会选择哪一家公司？说明理由；
（2）某课外实习作业小组调查了1000名职场人士，就选择这两家公司的意愿作了统计，得到如下数据分布：
若分析选择意愿与年龄这两个分类变量，计算得到的
的观测值为
，测得出“选择意愿与年龄有关系”的结论犯错误的概率的上限是多少？并用统计学知识分析，选择意愿与年龄变量和性别变量哪一个关联性更大？
附： 
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)的导函数f′(x)，且对任意x＞0，都有f′(x)＞
.
(1)判断函数F(x)＝
在(0，＋∞)上的单调性；
(2)设x1，x2∈(0，＋∞)，证明：f(x1)＋f(x2)＜f(x1＋x2)；
(3)请将(2)中结论推广到一般形式，并证明你所推广的结论．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
