
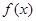 满足:对任意
满足:对任意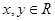 ,都有
,都有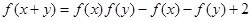 成立,且
成立,且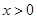 时,
时,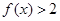 .
.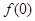 的值,并证明:当
的值,并证明:当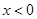 时,
时,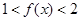 ;
;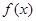 的单调性并加以证明;
的单调性并加以证明;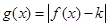 在
在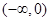 上递减,求实数
上递减,求实数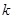 的取值范围.
的取值范围.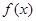 在
在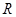 上是增函数;(3)
上是增函数;(3)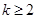
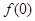 的值。
的值。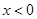 ,则
,则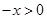 ,那么
,那么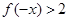 .用赋值法令
.用赋值法令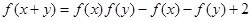 中的
中的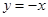 ,整理出
,整理出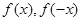 的关系式,用
的关系式,用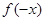 表示出
表示出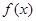 ,因为有
,因为有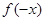 的范围所以可求出
的范围所以可求出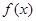 的范围。(2)由(1)知
的范围。(2)由(1)知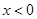 时,
时,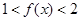 ,
,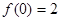 ,
,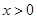 时,
时,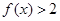 ,所以在R上
,所以在R上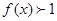 。在R上任取两个实数并可设
。在R上任取两个实数并可设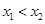 ,根据已知
,根据已知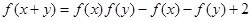 可用配凑法令
可用配凑法令 在代入上式找出
在代入上式找出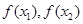 的关系。在比较
的关系。在比较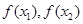 的大小时,在本题中采用作商法与1比较大小。(3)由(2)知函数
的大小时,在本题中采用作商法与1比较大小。(3)由(2)知函数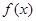 在
在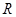 上是增函数。当
上是增函数。当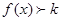 时
时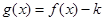 ,函数
,函数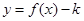 在
在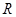 上也是增函数,不合题意故舍。当
上也是增函数,不合题意故舍。当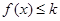 时
时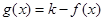 在
在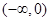 上单调递减,此时只需
上单调递减,此时只需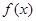 的最大值小于等于k即可。
的最大值小于等于k即可。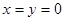 ,则
,则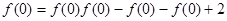 ,
,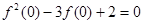 ,解得
,解得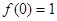 或
或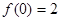
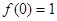 ,令
,令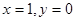 ,则
,则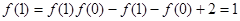 ,
,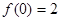
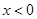 ,则
,则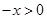 ,那么
,那么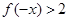 .
.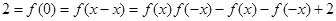
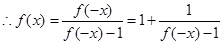
 ,从而
,从而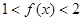 .
.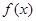 在
在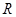 上是增函数.
上是增函数.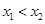 ,由(1)可知对任意
,由(1)可知对任意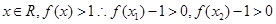
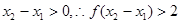
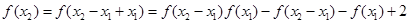
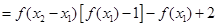
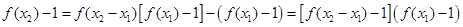
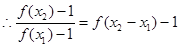
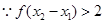
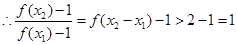
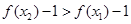 ,即
,即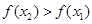
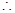 函数
函数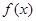 在
在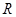 上是增函数。
上是增函数。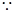 由(2)知函数
由(2)知函数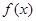 在
在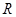 上是增函数.
上是增函数.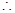 函数
函数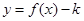 在
在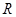 上也是增函数,
上也是增函数,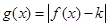 在
在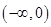 上递减,
上递减,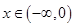 时,
时,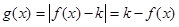 ,
,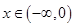 时,
时,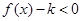 .
.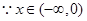 时,
时,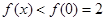
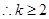


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源:不详 题型:解答题
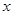 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当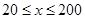 时,车流速度
时,车流速度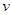 是车流密度x的一次函数.
是车流密度x的一次函数.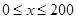 时,求函数
时,求函数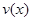 的表达式;
的表达式;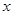 为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)
为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时) 可以达到最大,并求出最大值(精确到1辆/小时)
可以达到最大,并求出最大值(精确到1辆/小时)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com