
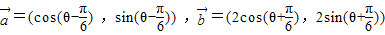 .
.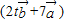 与向量
与向量 的夹角为锐角,求实数t的取值范围;
的夹角为锐角,求实数t的取值范围;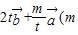 为常数,且m>0)的模的最小值.
为常数,且m>0)的模的最小值. ,
, ,
, ,由夹角为锐角,代入
,由夹角为锐角,代入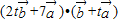 =2t|
=2t|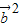 |
| >0,解不等式可求t的范围,舍去
>0,解不等式可求t的范围,舍去 =
= 中t即可
中t即可 =
=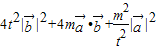 =
= ,结合y=
,结合y=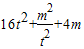 ,t∈(0,1]的单调性可求y的最小值
,t∈(0,1]的单调性可求y的最小值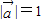 ,|
,| |=2,
|=2, =
= =1
=1 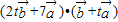 =
= =2t|
=2t| |2
|2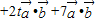 +7t
+7t >0
>0 或 t<-7
或 t<-7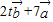 与
与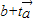 共线时,不满足题意.
共线时,不满足题意. =
=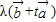
 ∴
∴
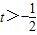 或 t<-7,且t
或 t<-7,且t (6分)
(6分) =
=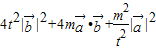

 t∈(0,1]
t∈(0,1] ≥8m+4m=12m
≥8m+4m=12m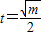
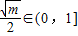 即 0<m≤4时
即 0<m≤4时 时,ymin=12m.从而
时,ymin=12m.从而
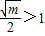 即m>4时
即m>4时 在(0,1]为减函数
在(0,1]为减函数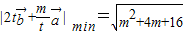 (6分)
(6分) 的夹角θ为锐角时,并不等价于
的夹角θ为锐角时,并不等价于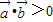 ,一定要把向量同向的情况去掉,及函数的单调性在求解函数最值中的应用.
,一定要把向量同向的情况去掉,及函数的单调性在求解函数最值中的应用. 

科目:高中数学 来源: 题型:
| 4 |
| 17 |
| a |
| ON |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| i |
| j |
| a |
| i |
| j |
| b |
| i |
| j |
| a |
| b |
| n |
| MP |
| MQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
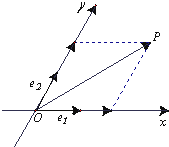 如图,设Ox,Oy是平面内相交成60°角的两条数轴,
如图,设Ox,Oy是平面内相交成60°角的两条数轴,| e1 |
| e2 |
| OP |
| e1 |
| e2 |
| OP |
| OA |
| OB |
| e1 |
| OA |
| e1 |
| OB |
| 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| i |
| j |
| OB1 |
| i |
| j |
| BnBn+1 |
| i |
| j |
| OB1 |
| B2B3 |
| OBn |
| OBn |
| i |
| j |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)若向量a与b反向,则a-b与a的方向_________,且|a-b|_________|a|+|b|;
(2)若a与b同向,且|a|>|b|则a-b与a的方向_________且|a-b|_________|a|-|b|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com