
(08年惠州一中五模理)如图,棱锥P―ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=![]() .
.
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)求二面角P―CD―B的大小;
(Ⅲ)求点C到平面PBD的距离.

方法一:
证:(Ⅰ)在Rt△BAD中,AD=2,BD=![]() ,
,
∴AB=2,ABCD为正方形,
因此BD⊥AC.
∵PA⊥平面ABCD,BDÌ平面ABCD,
∴BD⊥PA .
又∵PA∩AC=A
∴BD⊥平面PAC.
解:(Ⅱ)由PA⊥面ABCD,知AD为PD在平面ABCD的射影,又CD⊥AD,
∴CD⊥PD,知∠PDA为二面角P―CD―B的平面角.
又∵PA=AD,
∴∠PDA=450 .
(Ⅲ)∵PA=AB=AD=2
∴PB=PD=BD=![]()
设C到面PBD的距离为d,由![]() ,
,
有![]() ,
,
即![]() ,
,
得![]()
方法二:
证:(Ⅰ)建立如图所示的直角坐标系,
则A(0,0,0)、D(0,2,0)、P(0,0,2).
在Rt△BAD中,AD=2,BD=![]() ,
,
∴AB=2.
∴B(2,0,0)、C(2,2,0),
∴![]()
∵![]()
即BD⊥AP,BD⊥AC,又AP∩AC=A,
∴BD⊥平面PAC.
解:(Ⅱ)由(Ⅰ)得![]() .
.
设平面PCD的法向量为![]() ,则
,则![]() ,
,
即![]() ,∴
,∴![]()
故平面PCD的法向量可取为![]()
∵PA⊥平面ABCD,∴![]() 为平面ABCD的法向量.
为平面ABCD的法向量.
设二面角P―CD―B的大小为q,依题意可得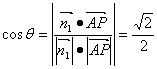 ,
,
∴q = 450 .
(Ⅲ)由(Ⅰ)得![]()
设平面PBD的法向量为![]() ,则
,则![]() ,
,
即![]() ,∴x=y=z
,∴x=y=z
故平面PBD的法向量可取为![]() .
.
∵![]() ,
,
∴C到面PBD的距离为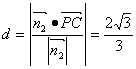



科目:高中数学 来源: 题型:
(08年惠州一中五模理) 甲、乙两人各射击一次,击中目标的概率分别是![]() 和
和![]() .假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响.
.假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响.
(Ⅰ)求甲射击4次,至少1次未击中目标的概率;
(Ⅱ)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(Ⅲ)假设某人连续2次未击中目标,则停止射击.问:乙恰好射击5次后,被中止射击的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年惠州一中五模理) 已知函数![]() 的图象为曲线E.
的图象为曲线E.
(Ⅰ) 若曲线E上存在点P,使曲线E在P点处的切线与x轴平行,求a,b的关系;
(Ⅱ) 说明函数![]() 可以在
可以在![]() 和
和![]() 时取得极值,并求此时a,b的值;
时取得极值,并求此时a,b的值;
(Ⅲ) 在满足(2)的条件下,![]() 在
在![]() 恒成立,求c的取值范围.
恒成立,求c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年惠州一中五模理) 已知椭圆的一个焦点![]() ,对应的准线方程为
,对应的准线方程为![]() ,且离心率
,且离心率![]() 满足
满足![]() ,
,![]() ,
,![]() 成等比数列.
成等比数列.
(1)求椭圆的方程;
(2)试问是否存在直线![]() ,使
,使![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() 、
、![]() ,且线段
,且线段![]() 恰被直线
恰被直线![]() 平分?若存在,求出
平分?若存在,求出![]() 的倾斜角的取值范围;若不存在,请说明理由.
的倾斜角的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com