
【题目】某市有一面积为12000平方米的三角形地块![]() ,其中边
,其中边![]() 长为200米,现计划建一个如图所示的长方形停车场
长为200米,现计划建一个如图所示的长方形停车场![]() ,停车场的四个顶点都在
,停车场的四个顶点都在![]() 的三条边上,其余的地面全部绿化.若建停车场的费用为180元/平方米,绿化的费用为60元/平方米,设
的三条边上,其余的地面全部绿化.若建停车场的费用为180元/平方米,绿化的费用为60元/平方米,设![]() 米,建设工程的总费用为
米,建设工程的总费用为![]() 元.
元.
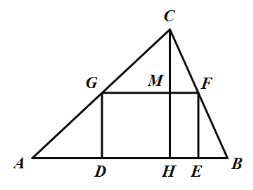
(1)求![]() 关于
关于![]() 的函数表达式:
的函数表达式:
(2)求停车场面积最大时![]() 的值,并求此时的工程总费用.
的值,并求此时的工程总费用.
科目:高中数学 来源: 题型:
【题目】折纸是一项艺术,可以折出很多数学图形.将一张圆形纸片放在平面直角坐标系中,圆心B(-1,0),半径为4,圆内一点A为抛物线![]() 的焦点.若每次将纸片折起一角,使折起部分的圆弧的一点
的焦点.若每次将纸片折起一角,使折起部分的圆弧的一点![]() 始终与点A重合,将纸展平,得到一条折痕,设折痕与线段
始终与点A重合,将纸展平,得到一条折痕,设折痕与线段![]() B的交点为P.
B的交点为P.
(Ⅰ)将纸片展平后,求点P的轨迹C的方程;
(Ⅱ)已知过点A的直线l与轨迹C交于R,S两点,当l无论如何变动,在AB所在直线上存在一点T,使得![]() 所在直线一定经过原点,求点T的坐标.
所在直线一定经过原点,求点T的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正四面体是侧棱与底面边长都相等的正三棱锥,它的对棱互相垂直.有一个如图所示的正四面体![]() ,E,F,G分别是棱AB,BC,CD的中点.
,E,F,G分别是棱AB,BC,CD的中点.

(1)求证:![]() 面EFG;
面EFG;
(2)求异面直线EG与AC所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生产企业研发了一种新产品,该新产品在某网店试销一个阶段后得到销售单价![]() 和月销售量
和月销售量![]() 之间的一组数据,如下表所示:
之间的一组数据,如下表所示:
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 |
月销售量 | 11 | 10 | 8 | 6 | 5 |
(Ⅰ)根据统计数据,求出![]() 关于
关于![]() 的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
(Ⅱ)生产企业与网店约定:若该新产品的月销售量不低于10万件,则生产企业奖励网店1万元;若月销售量不低于8万件且不足10万件,则生产企业奖励网店5000元;若月销售量低于8万件,则没有奖励.现用样本估计总体,从上述5个销售单价中任选2个销售单价,求抽到的产品含有月销量量不低于10万件的概率.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为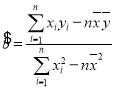 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产![]() ,
,![]() ,
,![]() 三种纪念品,每种纪念品均有普通型和精品型两种,某一天产量如下表(单位:个):
三种纪念品,每种纪念品均有普通型和精品型两种,某一天产量如下表(单位:个):
普通型 | 精品型 | |
纪念品 | 800 | 200 |
纪念品 |
| 150 |
纪念品 | 500 | 350 |
现采用分层抽样的方法在这一天生产的纪念品中抽取100个,其中有![]() 种纪念品40个.
种纪念品40个.
(1)若再用分层抽样的方法在所有![]() 种纪念品中抽取一个容量为13的样本.将该样本看成一个总体,从中任取2个纪念品,求至少有1个精品型纪念品的概率(用最简分数表示);
种纪念品中抽取一个容量为13的样本.将该样本看成一个总体,从中任取2个纪念品,求至少有1个精品型纪念品的概率(用最简分数表示);
(2)从![]() 种精品型纪念品中抽取6个,其某种指标的数据分别如下:4,7,
种精品型纪念品中抽取6个,其某种指标的数据分别如下:4,7,![]() ,
,![]() ,8,5.把这6个数据看作一个总体,其均值为7、方差为6,求
,8,5.把这6个数据看作一个总体,其均值为7、方差为6,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》卷五《商功》中有如下叙述“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈“刍甍”指的是底面为矩形的对称型屋脊状的几何体,“下广三丈”是指底面矩形宽三丈,“袤四丈”是指底面矩形长四丈,“上袤二丈”是指脊长二丈,“无宽”是指脊无宽度,“高一丈”是指几何体的高为一丈.现有一个刍甍如图所示,下广三丈,袤四丈,上袤三丈,无广,高二丈,则该刍甍的外接球的表面积为_______________平方丈.
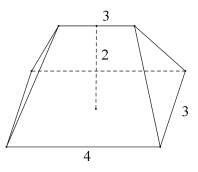
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com