
从6名短跑运动员中选出4人参加4×100 m接力赛.试求满足下列条件的参赛方案各有多少种?
(1)甲不能跑第一棒和第四棒;
(2)甲不能跑第一棒,乙不能跑第四棒
(1)240;(2)252;
解析试题分析:(1)可优先考虑特殊元素甲,此时务必注意甲是否参赛,因此需分两类,甲参赛和甲不参赛,利用分类加法计数原理求解
(2)显然第一、四棒为特殊位置,与之相伴的甲、乙则为特殊元素,这时特殊元素与特殊位置的个数相等,利用特殊位置(元素)优先考虑的原则解之.
(1)优先考虑特殊元素甲,让其选位置,此时务必注意甲是否参赛,因此需分两类:
第1类,甲不参赛有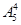 种排法;
种排法;
第2类,甲参赛,因只有两个位置可供选择,故有A种排法;其余5人占3个位置有A种排法,故有AA种方案.所以有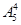 +
+
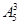 =240种参赛方案.
=240种参赛方案.
(2)优先考虑特殊位置.
第1类,乙跑第一棒有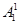
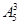 =60种排法;
=60种排法;
第2类,乙不跑第一棒有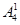
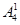
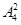 =192种排法.
=192种排法.
故共有60+192=252种参赛方案.
考点:排列组合,计数原理


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
6个人坐在一排10个座位上,则(用数字表示).
(1)空位不相邻的坐法有多少种?
(2)4个空位只有3个相邻的坐法有多少种?
(3)4个空位至多有2个相邻的坐法有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知(1+x)n=a0+a1(x-1)+a2(x-1)2+…+an(x-1)n(n∈N*).
(1)求a0及Sn=a1+a2+a3+…+an;
(2)试比较Sn与(n-2)2n+2n2的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工程队有6项工程需要先后单独完成,其中工程乙必须在工程甲完成后才能进行,工程丙必须在工程乙完成后才能进行,又工程丁必须在工程丙完成后立即进行.求安排这6项工程的不同排法种数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com