练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知f（x）是定义在R上的奇函数，且满足f（x+2）=﹣ ，当1≤x≤2时，f（x）=x，则f（﹣ ）= ．

    【答案】﹣
    【解析】解：由f（x+2）=﹣ ，得f（x+4）=﹣ =f（x），
    ∴f（x）是周期为4的奇函数，又当1≤x≤2时，f（x）=x，
    ∴f（﹣ ）=﹣f（ ）=﹣f（4+ ）=﹣f（ ）=﹣ ．
    所以答案是：- ．
    【考点精析】解答此题的关键在于理解函数奇偶性的性质的相关知识，掌握在公共定义域内，偶函数的加减乘除仍为偶函数；奇函数的加减仍为奇函数；奇数个奇函数的乘除认为奇函数；偶数个奇函数的乘除为偶函数；一奇一偶的乘积是奇函数;复合函数的奇偶性：一个为偶就为偶，两个为奇才为奇，以及对函数的值的理解，了解函数值的求法：①配方法(二次或四次)；②“判别式法”；③反函数法；④换元法；⑤不等式法；⑥函数的单调性法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在用“五点法”画函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜ ）在某一周期内的图象时，列表并填入了部分数据，如下表：

    ωx+φ

    0

    π

    2π

    x

    π

    Asin（ωx+φ）

    0

    3

    ﹣3

    0


    （1）请将上表空格中处所缺的数据填写在答题卡的相应位置上，并直接写出函数f（x）的解析式；
    （2）将y=f（x）图象上所有点的横坐标缩短为原来的 ，再将所得图象向左平移 个单位，得到y=g（x）的图象，求g（x）的单调递增区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左右焦点分别为，点为椭圆上一点. 的重心为，内心为，且，则该椭圆的离心率为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等差数列的前三项依次为a,3,5a，前n项和为Sn，且Sk＝121.

    (1)求a及k的值；

    (2)设数列{bn}的通项bn＝，证明数列{bn}是等差数列，并求其前n项和Tn.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，三棱台 中，，分别为AC，CB的中点．

    （1）求证：平面；

    （2）若，，求证：平面 平面.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

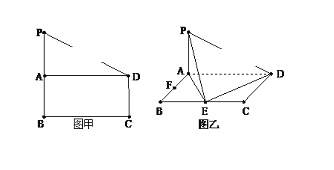
    【题目】如图甲，在直角梯形PBCD中，PB∥CD，CD⊥BC，BC＝PB＝2CD，A是PB的中点．

    现沿AD把平面PAD折起，使得PA⊥AB（如图乙所示），E、F分别为BC、AB边的中点．

    （1）求证：平面PAE⊥平面PDE；

    （2）在PE上找一点Q，使得平面BDQ⊥平面ABCD．

    （3）在PA上找一点G，使得FG∥平面PDE．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知四棱台的上下底面分别是边长为和的正方形，且底面，点为的中点,在边上，且.

    （1）求证：∥平面；

    （2）求证： .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】连接球面上两点的线段称为球的弦，半径为4的球的两条弦AB，CD的长度分别为2 和4 ，M，N分别是AB，CD的中点，两条弦的两端都在球面上运动，有下面四个命题：
    ①弦AB，CD可能相交于点M；
    ②弦AB，CD可能相交于点N；
    ③MN的最大值是5；
    ④MN的最小值是1；
    其中所有正确命题的序号为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】解关于x的不等式：(a＋1)x2－(2a＋3)x＋2<0.

    查看答案和解析>>

    同步练习册答案