
分析 (1)当a=0,且b≠0时,可得c=-$\frac{b}{2}$,方程即bx-$\frac{b}{2}$=0,由此求得x的值.
(2)由题意可得f(0)=c<0,故只需证f(1)=a+b+c>0.再根据f(1)=a+b+c,它与3a+3b+3c同号.把3b=-2a-6c代入3a+3b+3c求得它等于a-3c>0,故有f(1)=a+b+c>0,根据函数零点的判定定理,得出结论.
解答 解:(1)当a=0,且b≠0时,关于x的方程ax2+bx+c=0,其中2a+3b+6c=0,
可得c=-$\frac{b}{2}$,方程即bx-$\frac{b}{2}$=0,求得x=$\frac{1}{2}$.
(2)当a>0,c<0时,设f(x)=ax2+bx+c,∵f(0)=c<0,故只需证f(1)=a+b+c>0.
再根据f(1)=a+b+c,它与3a+3b+3c同号.
由2a+3b+6c=0,可得3b=-2a-6c,故有3a+3c-2a-6c=a-3c>0,故有f(1)=a+b+c>0,
可得f(0)f(1)<0,根据函数零点的判定定理,f(x)必有一个根在(0,1)内,
即方程ax2+bx+c=0必有一根在(0,1)内.
点评 本题主要考查一元二次方程根的分布与系数的关系,二次函数的性质,体现了转化的数学思想,属于中档题.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:选择题
| x | -1 | 0 | 1 | 2 | 3 |
| f(x) | -0.677 | 3.011 | 5.432 | 5.980 | 7.651 |
| g(x) | -0.530 | 3.451 | 4.890 | 5.241 | 6.892 |
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AB=4,BC=3,CD=2,DA=1,四边形的四个角分别记为A,B,C,D.
如图,在四边形ABCD中,AB=4,BC=3,CD=2,DA=1,四边形的四个角分别记为A,B,C,D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
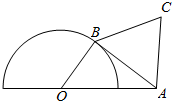 如图所示,半圆O的直径为2,A为半圆直径的延长线上的一点,且OA=2,B为半圆上任一点,以AB为边向右上方作等边△ABC.
如图所示,半圆O的直径为2,A为半圆直径的延长线上的一点,且OA=2,B为半圆上任一点,以AB为边向右上方作等边△ABC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3) | B. | (3,1) | C. | (7,12) | D. | (12,7) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com