
【题目】下列命题正确的个数为( )
(1)已知定点![]() 满足
满足![]() ,动点P满足
,动点P满足![]() ,则动点P的轨迹是椭圆;
,则动点P的轨迹是椭圆;
(2)已知定点![]() 满足
满足![]() ,动点M满足
,动点M满足![]() ,则动点M的轨迹是一条射线;
,则动点M的轨迹是一条射线;
(3)当1<k<4时,曲线C:![]() =1表示椭圆;
=1表示椭圆;
(4)若动点M的坐标满足方程![]() ,则动点M的轨迹是抛物线。
,则动点M的轨迹是抛物线。
A. 0个B. 1个C. 2个D. 3个
【答案】B
【解析】
(1)当P不在直线F1F2上时或在直线F1F2上且在F1、F2两点之外时,都有|PF1|+|PF2|>|F1F2|,只有点P在直线F1F2上且在F1、F2两点之间(或与F1、F2重合)时,符合题意.由此得到答案.
(2)根据条件结合双曲线的定义只有点M在直线F1F2上且在F1、F2两点之外时才满足![]() ,由此得到一条射线.
,由此得到一条射线.
(3)根据曲线方程的特点,结合椭圆、圆的标准方程分别判断即可.
(4)把已知方程变形为![]() ,此式不满足抛物线的定义,从而得到答案.
,此式不满足抛物线的定义,从而得到答案.
(1)∵|PF1|+|PF2|=8,且|F1F2|=8
∴|PF1|+|PF2|=|F1F2|,只有当点P在直线F1F2上且在F1、F2两点之间(或与F1、F2重合)时,符合题意.∴点P的轨迹是线段F1F2.故(1)错误.
(2)∵|F1F2|=8,在平面内动点M满足|MF1|﹣|MF2|=8=|F1F2|,∴点M在直线F1F2上且在点F1F2的延长线上时符合题意.∴M点的轨迹是一条射线,故(2)正确.
(3)当k![]() 时,4﹣k=k﹣1,此时曲线表示为圆,∴(3)错误.
时,4﹣k=k﹣1,此时曲线表示为圆,∴(3)错误.
(4)∵动点M的坐标满足方程5![]() |3x+4y|,变形为
|3x+4y|,变形为![]() ,
,
∴上式表示的是动点M(x,y)到定点(0,0)与定直线3x+4y=0的距离相等,但定点(0,0)在定直线3x+4y=0上,不满足抛物线的定义,所以动点M的轨迹是一条直线.故(4)错误.
综上,正确的只有(2),
故选:B.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:
【题目】如图1,在△ABC中,D,E分别为AB,AC的中点,O为DE的中点,![]() ,BC=4.将△ADE沿DE折起到△
,BC=4.将△ADE沿DE折起到△![]() 的位置,使得平面
的位置,使得平面![]() 平面BCED, F为A1C的中点,如图2.
平面BCED, F为A1C的中点,如图2.

(1)求证EF∥平面![]() ;
;
(2)求点C到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD-A1B1C1D1中,M、N分别为棱BC和棱CC1的中点,则异面直线AC和MN所成的角为( )
A. 30° B. 45° C. 90° D. 60°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在下列命题中:
①方程![]() 表示的曲线所围成区域面积为
表示的曲线所围成区域面积为![]() ;
;
②与两坐标轴距离相等的点的轨迹方程为![]() ;
;
③与两定点![]() 距离之和等于
距离之和等于![]() 的点的轨迹为椭圆;
的点的轨迹为椭圆;
④与两定点![]() 距离之差的绝对值等于1的点的轨迹为双曲线.
距离之差的绝对值等于1的点的轨迹为双曲线.
正确的命题的序号是________.(注:把你认为正确的命题序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱![]() 的底面边长和侧棱长均为2,
的底面边长和侧棱长均为2,![]() 为棱
为棱![]() 的中点 .
的中点 .
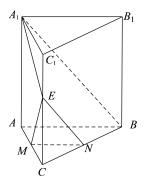
(1)证明:平面![]() 平面
平面![]() ;
;
(2)是否存在平行于![]() 的动直线
的动直线![]() ,分别与棱
,分别与棱![]() 交于点
交于点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() ,若存在,求出点
,若存在,求出点![]() 到直线
到直线![]() 的距离;若不存在,说明理由.
的距离;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com