
【题目】已知圆C同时满足下列三个条件:①与y轴相切;②在直线y=x上截得弦长为2 ![]() ;③圆心在直线x﹣3y=0上.求圆C的方程.
;③圆心在直线x﹣3y=0上.求圆C的方程.
【答案】解:设所求的圆C与y轴相切,又与直线y=x交于AB, ∵圆心C在直线x﹣3y=0上,∴圆心C(3a,a),又圆
与y轴相切,∴R=3|a|.又圆心C到直线y﹣x=0的距离 ![]() .
.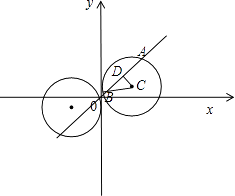
在Rt△CBD中, ![]() ,
,
∴9a2﹣2a2=7.a2=1,a=±1,3a=±3.
∴圆心的坐标C分别为(3,1)和(﹣3,﹣1),
故所求圆的方程为(x﹣3)2+(y﹣1)2=9或(x+3)2+(y+1)2=9
【解析】设所求的圆C与y轴相切,又与直线y=x交于AB,由题设知圆心C(3a,a),R=3|a|,再由点到直线的距离公式和勾股定理能够求出a的值,从而得到圆C的方程.
【考点精析】解答此题的关键在于理解圆的标准方程的相关知识,掌握圆的标准方程:![]() ;圆心为A(a,b),半径为r的圆的方程.
;圆心为A(a,b),半径为r的圆的方程.


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】如图所示,过抛物线C:y2=2px(p>0)的焦点F作直线交C于A、B两点,过A、B分别向C的准线l作垂线,垂足为A′,B′,已知四边形AA′B′F与BB′A′F的面积分别为15和7,则△A′B′F的面积为 . 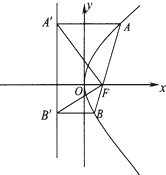
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)如图,曲线![]() 由上半椭圆
由上半椭圆![]() 和部分抛物线
和部分抛物线![]()
![]() 连接而成,
连接而成, ![]() 的公共点为
的公共点为![]() ,其中
,其中![]() 的离心率为
的离心率为![]() .
.

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)过点![]() 的直线
的直线![]() 与
与![]() 分别交于
分别交于![]() (均异于点
(均异于点![]() ),若
),若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l经过直线3x+4y﹣2=0与直线2x+y+2=0的交点P,且垂直于直线x﹣2y﹣1=0.求:
(Ⅰ)直线l的方程;
(Ⅱ)直线l与两坐标轴围成的三角形的面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,且此函数图象过点(1,5).
,且此函数图象过点(1,5).
(1)求实数m的值;
(2)判断f(x)奇偶性;
(3)讨论函数f(x)在[2,+∞)上的单调性?并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(x+1),g(x)=loga ![]() ,(a>0且a≠1).记F(x)=2f(x)+g(x).
,(a>0且a≠1).记F(x)=2f(x)+g(x).
(1)求函数F(x)的零点;
(2)若关于x的方程F(x)﹣2m2+3m+5=0在区间[0,1)内仅有一解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C1:y2=8x与双曲线C2: ![]() (a>0,b>0)有公共焦点F2 , 点A是曲线C1 , C2在第一象限的交点,且|AF2|=5.
(a>0,b>0)有公共焦点F2 , 点A是曲线C1 , C2在第一象限的交点,且|AF2|=5.
(1)求双曲线C2的方程;
(2)以双曲线C2的另一焦点F1为圆心的圆M与直线y= ![]() 相切,圆N:(x﹣2)2+y2=1.过点P(1,
相切,圆N:(x﹣2)2+y2=1.过点P(1, ![]() )作互相垂直且分别与圆M、圆N相交的直线l1和l2 , 设l1被圆M截得的弦长为s,l2被圆N截得的弦长为t,问:
)作互相垂直且分别与圆M、圆N相交的直线l1和l2 , 设l1被圆M截得的弦长为s,l2被圆N截得的弦长为t,问: ![]() 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长郡中学学习兴趣小组通过随机询问某地100名高中学生在选择座位时是否挑同桌,得到如下![]() 列联表:
列联表:
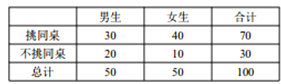
(1)从这50名男生中按是否挑同桌采取分层抽样的方法抽取一个容量为5的样本,现从这5人中随机选取3人做深层采访,求这3名学生中至少有2名要挑同桌的概率;
(2)根据以上![]() 列联表,是否有95%以上的把握认为“性别与在选择座位时是否挑同桌”有关?下面的临界值表仅供参考:
列联表,是否有95%以上的把握认为“性别与在选择座位时是否挑同桌”有关?下面的临界值表仅供参考:

(参考公式: 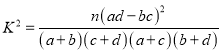 ,其中
,其中![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com