练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    将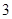个不同的小球放入个盒子中，则不同放法种数有（  ）

    A．B．C．D．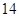

    B

    解析试题分析：一个小球有4种不同的方法，第二个小球也有4种不同的方法，第三个小球也有4种不同的放法，即每个小球都有4种可能的放法，根据分步乘法原理得到结果。解：本题是一个分步计数问题
    对于第一个小球有4众不同的方法，第二个小球也有4众不同的方法，第三个小球也有4众不同的放法，即每个小球都有4种可能的放法，根据分步计数原理知共有即4×4×4=64，故选B
    考点：分步计数原理
    点评：本题考查分步计数原理，是一个典型的分步计数问题，本题对于盒子和小球没有任何限制条件，可以把小球随便放置，注意与有限制条件的元素的问题的解法

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：单选题

    设，那么的值为（  ）

    A．－B．－C．－D．—1

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    有七名同学站成一排照毕业纪念照，其中甲不能和乙站在一起，并且乙、丙两位同学要站在一起，则不同的站法有（　　）

    A．1200种 B．1330种 C．1320种 D．600种

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    用数字1,2,3,4组成数字可以重复的四位数，其中有且只有一个数字出现两次的四位数的个数为

    A．144B．120C．108D．72

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    二项式的展开式的第二项的系数为，则的值为

    A．B．C．或D．或

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    已知二项式的展开式中第4项为常数项，则项的系数为（   ）

    A．-19B．19C．20D．-20

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    有编号分别为1，2，3，4，5的5个红球和5个黑球，从中取出4个，则取出的编号互不相同的种数为（    ）                                                           

    A．5 B．80 C．105 D．210

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    高三某班团支部换届进行差额选举，从已产生的甲、乙、丙、丁四名候选人中选出三人分别担任书记、组织委员和宣传委员，并且要求乙是上届组织委员不能连任原职，则换届后不同的任职结果有

    A．16种 B．18种 C．20种 D．22种

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    二项式的展开式的常数项为第（    ）项

    A．17 B．18
    C．19 D．20

    查看答案和解析>>

    同步练习册答案