
【题目】已知函数f(x)=![]() sin 2x-
sin 2x-![]() cos2x.
cos2x.
(1)求f(x)的周期和最小值;
(2)将函数f(x)的图像上每一点的横坐标伸长到原来的两倍(纵坐标不变),再把所得图像上的所有点向上平移![]() 个单位,得到函数g(x)的图像,当
个单位,得到函数g(x)的图像,当![]() 时,求g(x)的值域.
时,求g(x)的值域.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 离心率为
离心率为![]() ,两准线之间的距离为8,点
,两准线之间的距离为8,点![]() 在椭圆
在椭圆![]() 上,且位于第一象限,过点
上,且位于第一象限,过点![]() 作直线
作直线![]() 的垂线
的垂线![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线
的垂线![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 的交点
的交点![]() 在椭圆
在椭圆![]() 上,求点
上,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为圆
为圆![]() 的圆心,
的圆心, ![]() 是圆上的动点,点
是圆上的动点,点![]() 在圆的半径
在圆的半径![]() 上,且有点
上,且有点![]() 和
和![]() 上的点
上的点![]() ,满足
,满足![]() ,
, ![]() .
.
(1)当点![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹方程;
的轨迹方程;
(2)若斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 相切,直线
相切,直线![]() 与(1)中所求点
与(1)中所求点![]() 的轨迹交于不同的两点
的轨迹交于不同的两点![]() ,
, ![]() ,
, ![]() 是坐标原点,且
是坐标原点,且![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C:ρsin2θ=2acos θ(a>0),过点P(-2,-4)的直线l的参数方程为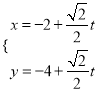 ,直线l与曲线C分别交于M,N两点.若|PM|,|MN|,|PN|成等比数列,则a的值为________.
,直线l与曲线C分别交于M,N两点.若|PM|,|MN|,|PN|成等比数列,则a的值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半径为2的圆内有两条圆弧,一质点M自点A开始沿弧A-B-C-O-A-D-C做匀速运动,则其在水平方向(向右为正)的速度![]() 的图像大致为( )
的图像大致为( )


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016·武昌调研)如图,在圆内画1条线段,将圆分成2部分;画2条相交线段,将圆分割成4部分;画3条线段,将圆最多分割成7部分;画4条线段,将圆最多分割成11部分.则
![]()
(1)在圆内画5条线段,将圆最多分割成________部分;
(2)在圆内画n条线段,将圆最多分割成________部分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AD∥BC,CD⊥BC,AD=2,AB=BC=3,PA=4,M为AD的中点,N为PC上一点,且PC=3PN.
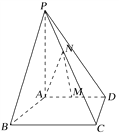
(1)求证:MN∥平面PAB;
(2)求点M到平面PAN的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com