
【题目】如图,四棱锥![]() ,
,![]() 平面
平面![]() ,且
,且![]() ,底面
,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,平面
的中点,平面![]() 与
与![]() 的交点为
的交点为![]() .
.
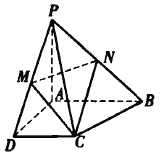
(1)求![]() 的长度;
的长度;
(2)求截面![]() 的底面
的底面![]() 所成二面角的大小;
所成二面角的大小;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设有2009个人站成一排,从第一名开始1至3报数,凡报到3的就退出队伍,其余的向前靠拢站成新的一排.再按此规则继续进行,直到第![]() 次报数后只剩下3人为止.试问:最后剩下的3人最初站在什么位置?
次报数后只剩下3人为止.试问:最后剩下的3人最初站在什么位置?
查看答案和解析>>
科目:高中数学 来源: 题型:
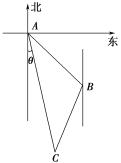
【题目】如图,甲船在A处,乙船在A处的南偏东45°方向,距A有9海里的B处,并以20海里每小时的速度沿南偏西15°方向行驶,若甲船沿南偏东θ度的方向,并以28海里每小时的速度行驶,恰能在C处追上乙船.问用多少小时追上乙船,并求sin θ的值.(结果保留根号,无需求近似值)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名篮球运动员,甲投篮一次命中的概率为![]() ,乙投篮一次命中的概率为
,乙投篮一次命中的概率为![]() ,若甲、乙各投篮三次,设
,若甲、乙各投篮三次,设![]() 为甲、乙投篮命中的次数的差的绝对值,其中甲、乙两人投篮是否命中相互没有影响.
为甲、乙投篮命中的次数的差的绝对值,其中甲、乙两人投篮是否命中相互没有影响.
(1)若甲、乙第一次投篮都命中,求甲获胜(甲投篮命中数比乙多)的概率;
(2)求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() (如图一)的平面展开图(如图二)中,
(如图一)的平面展开图(如图二)中,![]() 为边长等于
为边长等于![]() 的正方形,△
的正方形,△![]() 和△
和△![]() 均为正三角形,在三棱锥
均为正三角形,在三棱锥![]() 中,
中,

(1)求证:![]() ;
;
(2)求![]() 与平面
与平面![]() 所成的角的大小;
所成的角的大小;
(3)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义空间点到几何图形的距离为:这一点到这个几何图形上各点距离中最短距离.
(1)在空间,求与定点![]() 距离等于1的点所围成的几何体的体积和表面积;
距离等于1的点所围成的几何体的体积和表面积;
(2)在空间,线段![]() (包括端点)的长等于1,求到线段
(包括端点)的长等于1,求到线段![]() 的距离等于1的点所围成的几何体的体积和表面积;
的距离等于1的点所围成的几何体的体积和表面积;
(3)在空间,记边长为1的正方形![]() 区域(包括边界及内部的点)为
区域(包括边界及内部的点)为![]() ,求到
,求到![]() 距离等于1的点所围成的几何体的体积和表面积.
距离等于1的点所围成的几何体的体积和表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照![]() ,
,![]() ,…,
,…,![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
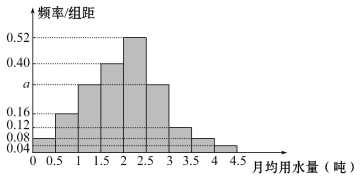
(1)求直方图中a的值.
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由.
(3)若该市政府希望使85%的居民每月的用水量不超过标准x(吨),估计x的值,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com