【题目】如图，在四棱锥
中， 
， 
平面
. 
为
的中点， 
.
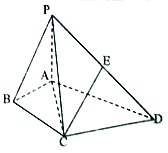
(1)求证： 
平面
；
(2)求三棱锥
的体积.
【答案】（1）见解析；（2）
【解析】试题分析：1）法一： 取AD得中点M，连接EM,CM.则EM//PA
因为
所以，EM∥平面PAB （2分）
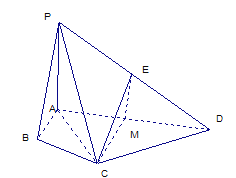
在Rt△ACD中， 
所以， 
而
,所以MC//AB （3分）
因为
所以， 
平面PAB （4分）
又因为
所以，平面EMC∥平面PAB
因为EC
平面EMC，∴EC∥平面PAB （6分）
法二： 延长DC,AB,交于N点，连接PN.
因为
所以C为ND的中点. （3分）
因为E为PD的中点，所以，EC//PN
因为
∴EC∥平面PAB （6分）
2）法一：由已知条件有;AC=2AB=2,AD=2AC=4,CD=
.（7分）
因为PA⊥平面ABCD，所以PA⊥CD （8分）
又因为CD⊥AC，AC∩PA=A，所以CD⊥平面PAC ..（10分）
因为E是PD的中点，所以点E平面PAC的距离h=
，
所以，四面体PACE的体积
（12分）
法二：由已知条件有;AC=2AB=2,AD=2AC=4,CD=
因为PA⊥平面ABCD，所以
.（10分）
因为E是PD的中点，所以，四面体PACE的体积
..（12分）
科目：高中数学 来源： 题型：
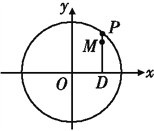
【题目】如图,设P是圆
上的动点,点D是P在x轴上的投影，M为线段PD上一点,且
，
(1)当P在圆上运动时,求点M的轨迹C的方程；
(2)求过点(3,0)且斜率为
的直线被轨迹C所截线段的长度.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某种产品的广告费支出
(百万元)与销售额
(百万元)之间有如下对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 50 | 60 | 70 |
如果
与
之间具有线性相关关系.
（1）作出这些数据的散点图；
（2）求这些数据的线性回归方程
;
（3）预测当广告费支出为9百万元时的销售额。 ( 参考数据： 
)
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】当今，手机已经成为人们不可或缺的交流工具，人们常常把喜欢玩手机的人冠上了名号“低头族”，手机已经严重影响了人们的生活，一媒体为调查市民对低头族的认识，从某社区的500名市民中，随机抽取
名市民，按年龄情况进行统计的频率分布表和频率分布直方图如图：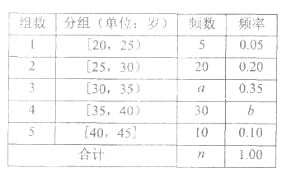
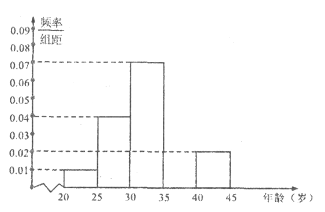
（1）求出表中的
的值，并补全频率分布直方图；
（2）媒体记者为了做好调查工作，决定从所随机抽取的市民中按年龄采用分层抽样的方法抽取20名接受采访，再从抽出的这20名中年龄在
的选取2名担任主要发言人．记这2名主要发言人年龄在
的人数为
，求
的分布列及数学期望．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设m，n是两条不同的直线，α、β是两个不同的平面，则下列命题不正确的是________．
（1）．若m⊥n，m⊥α，n
α，则n∥α
（2）．若m⊥β，α⊥β，则m∥α或m
α
（3）．若m⊥n，m⊥α，n⊥β，则α⊥β
（4）．若
∥α，α⊥β，则
⊥β
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】数列{an}的前n项和记为Sn ， a1=1，an+1=2Sn+1（n≥1）．
（1）求{an}的通项公式；
（2）等差数列{bn}的各项为正，其前n项和为Tn ， 且T3=15，又a1+b1 ， a2+b2 ， a3+b3成等比数列，求Tn ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
