
【题目】“冰桶挑战赛”是一项社交网络上发起的慈善公益活动,活动规定:被邀请者要么在![]() 小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外
小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外![]() 个人参与这项活动.假设每个人接受挑战与不接受挑战是等可能的,且互不影响.
个人参与这项活动.假设每个人接受挑战与不接受挑战是等可能的,且互不影响.
(1)若某参与者接受挑战后,对其他![]() 个人发出邀请,则这
个人发出邀请,则这![]() 个人中至少有
个人中至少有![]() 个人接受挑战的概率是多少?
个人接受挑战的概率是多少?
(2)为了解冰桶挑战赛与受邀者的性别是否有关,某调查机构进行了随机抽样调查,调查得到如下列联表:
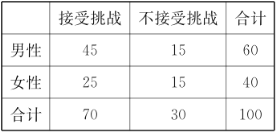
根据表中数据,能否有![]() %的把握认为“冰桶挑战赛与受邀者的性别有关”?
%的把握认为“冰桶挑战赛与受邀者的性别有关”?
附: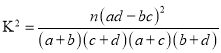

【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
试题(1)分别列出3人参加活动的所以可能结果,和其中至少有3人接受挑战的情况种数,然后根据古典概型的概率计算;(2)根据列联表中的数据计算观测值![]() ,然后和表中的
,然后和表中的![]() 进行比较,大于就表示有关,小于表示没有90%的把握认为“冰桶挑战赛与受邀者的性别有关”.
进行比较,大于就表示有关,小于表示没有90%的把握认为“冰桶挑战赛与受邀者的性别有关”.
试题解析:(1)这![]() 个人接受挑战分别记为
个人接受挑战分别记为![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() 分别表示这
分别表示这![]() 个人不接受挑战.
个人不接受挑战.
这![]() 个人参与该项活动的可能结果为:
个人参与该项活动的可能结果为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共有
,共有![]() 种.
种.
其中,至少有![]() 个人接受挑战的可能结果有:
个人接受挑战的可能结果有:![]() ,
,![]() ,
,![]() ,
,![]() ,共有
,共有![]() 种.
种.
根据古典概型的概率公式,所求的概率为![]() .
.
(2)根据![]() 列联表,得到
列联表,得到![]() 的观测值为:
的观测值为:

![]() .
.
因为![]() .
.
所以没有![]() %的把握认为“冰桶挑战赛与受邀者的性别有关”.
%的把握认为“冰桶挑战赛与受邀者的性别有关”.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某人在塔的正东方向沿着南偏西60°的方向前进40 m以后,望见塔在东北方向上,若沿途测得塔的最大仰角为30°,则塔高为________________m.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市A,B,C,D四所中学报名参加某高校2015年自主招生考试的学生人数如下表所示:
中学 | A | B | C | D |
人数 | 40 | 30 | 10 | 20 |
该市教委为了解参加考试的学生的学习状况,采用分层抽样的方法从四所中学报名参加考试的学生中随机抽取50名参加问卷调查.则A,B,C,D四所中学抽取的学生人数分别为( )
A.15,20,10,5B.15,20,5,10
C.20,15,10,5D.20,15,5,10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在甲、乙两个盒子中分别装有编号为1,2,3,4的四个形状相同的小球,现从甲、乙两个盒子中各取出2个小球,每个小球被取出的可能性相等.
(1)求从甲盒中取出的两个球上的编号不都是奇数的概率;
(2)求从甲盒取出的小球上编号之和与从乙盒中取出的小球上编号之和相等的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱锥![]() 的三条侧棱
的三条侧棱![]() ,
, ![]() ,
, ![]() 两两垂直,
两两垂直, ![]() 为等边三角形,
为等边三角形, ![]() 为
为![]() 内部一点,点
内部一点,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .
.
(Ⅰ)证明: ![]() ;
;
(Ⅱ)证明: ![]() ;
;
(Ⅲ)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网站举行“卫生防疫”的知识竞赛网上答题,共有120000人通过该网站参加了这次竞赛,为了解竞赛成绩情况,从中抽取了100人的成绩进行统计,其中成绩分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其频率分布直方图如图所示,请你解答下列问题:
,其频率分布直方图如图所示,请你解答下列问题:
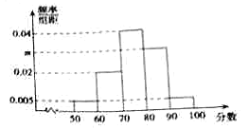
(1)求![]() 的值;
的值;
(2)成绩不低于90分的人就能获得积分奖励,求所有参赛者中获得奖励的人数;
(3)根据频率分布直方图,估计这次知识竞赛成绩的平均分(用组中值代替各组数据的平均值).
查看答案和解析>>
科目:高中数学 来源: 题型:
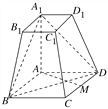
【题目】如图所示,在四棱台ABCDA1B1C1D1中,AA1⊥底面ABCD,四边形ABCD为菱形,∠BAD=120°,AB=AA1=2A1B1=2.
(1)若M为CD中点,求证:AM⊥平面AA1B1B;
(2)求直线DD1与平面A1BD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 过点
过点![]() ,且倾斜角为
,且倾斜角为![]() ,以坐标原点为极点,
,以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 的参数方程;
的参数方程;
(2)设直线![]() 与圆
与圆![]() 的两个交点分别为
的两个交点分别为![]() ,
, ![]() ,求证:
,求证: 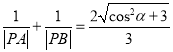 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com