
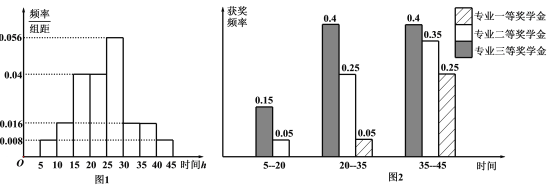
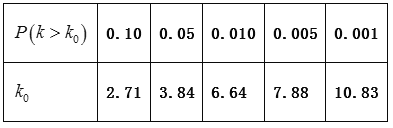
【题目】某“双一流”大学专业奖学金是以所学专业各科考试成绩作为评选依据,分为专业一等奖学金(奖金额![]() 元)、专业二等奖学金(奖金额
元)、专业二等奖学金(奖金额![]() 元)及专业三等奖学金(奖金额
元)及专业三等奖学金(奖金额![]() 元),且专业奖学金每个学生一年最多只能获得一次.图(1)是统计了该校
元),且专业奖学金每个学生一年最多只能获得一次.图(1)是统计了该校![]() 年
年![]() 名学生周课外平均学习时间频率分布直方图,图(2)是这
名学生周课外平均学习时间频率分布直方图,图(2)是这![]() 名学生在
名学生在![]() 年周课外平均学习时间段获得专业奖学金的频率柱状图.
年周课外平均学习时间段获得专业奖学金的频率柱状图.
(Ⅰ)求这![]() 名学生中获得专业三等奖学金的人数;
名学生中获得专业三等奖学金的人数;
(Ⅱ)若周课外平均学习时间超过![]() 小时称为“努力型”学生,否则称为“非努力型”学生,列
小时称为“努力型”学生,否则称为“非努力型”学生,列![]() 联表并判断是否有
联表并判断是否有![]() 的把握认为该校学生获得专业一、二等奖学金与是否是“努力型”学生有关?
的把握认为该校学生获得专业一、二等奖学金与是否是“努力型”学生有关?
(Ⅲ)若以频率作为概率,从该校任选一名学生,记该学生![]() 年获得的专业奖学金额为随机变量
年获得的专业奖学金额为随机变量![]() ,求随机变量
,求随机变量![]() 的分布列和期望.
的分布列和期望.
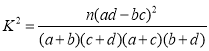
【答案】(Ⅰ)160人;(Ⅱ)有;(Ⅲ)见解析.
【解析】
(Ⅰ)根据频率之和为1,得到获得三等奖学金的频率,再由总人数得到答案;(Ⅱ)根据频率分布直方图和频率柱状图,填写好列联表,再计算出![]() 进行判断,得到答案;(Ⅲ)先得到
进行判断,得到答案;(Ⅲ)先得到![]() 可取的值,再分别求出其概率,根据数学期望的公式,得到答案.
可取的值,再分别求出其概率,根据数学期望的公式,得到答案.
![]() 获得三等奖学金的频率为:
获得三等奖学金的频率为:![]()
![]() ,
,
故这![]() 名学生获得专业三等奖学金的人数为
名学生获得专业三等奖学金的人数为![]() 人.
人.
![]() 每周课外学习时间不超过
每周课外学习时间不超过![]() 小时的“非努力型”学生有
小时的“非努力型”学生有![]()
其中获得一、二等奖学金学生有![]()
每周课外学习时间超过![]() 小时称为“努力型”学生有
小时称为“努力型”学生有![]() 人,
人,
其中获得一、二等奖学金学生有![]() 人,
人,
![]() 联表如图所示:
联表如图所示:
“非努力型”学生 | “努力型”学生 | 总计 | |
获得一二等奖学金学生 |
|
|
|
未获得一二等奖学金学生 |
|
|
|
总计 |
|
|
|
![]()
故有![]() 的把握认为获得一二等奖学金与学习“努力型”学生的学习时间有关;
的把握认为获得一二等奖学金与学习“努力型”学生的学习时间有关;
![]() 的可能取值为
的可能取值为![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() 的分布列
的分布列
| 0 | 600 | 1500 | 3000 |
| 0.424 | 0.32 | 0.198 | 0.058 |
其期望为![]() 元.
元.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD﹣A1B1C1D1中,底面ABCD是边长为2的正方形.
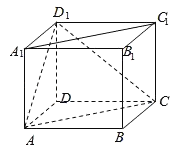
(1)证明:A1C1![]() 平面ACD1;
平面ACD1;
(2)求异面直线CD与AD1所成角的大小;
(3)已知三棱锥D1﹣ACD的体积为![]() ,求AA1的长.
,求AA1的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校学生社团组织活动丰富,学生会为了解同学对社团活动的满意程度,随机选取了100位同学进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[40,50),[50,60),[60,70),…,[90,100]分成6组,制成如图所示频率分布直方图.
(1)求图中x的值;
(2)求这组数据的中位数;
(3)现从被调查的问卷满意度评分值在[60,80)的学生中按分层抽样的方法抽取5人进行座谈了解,再从这5人中随机抽取2人作主题发言,求抽取的2人恰在同一组的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车公司为调查4S店个数对该公司汽车销量的影响,对同等规模的A,B,C,D四座城市的4S店一个月某型号汽车销量进行了统计,结果如下表:
城市 | A | B | C | D |
4S店个数x | 3 | 4 | 6 | 7 |
销售台数y | 18 | 26 | 34 | 42 |
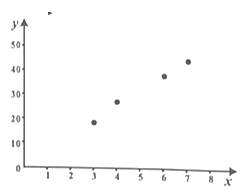
(1)由散点图知y与x具有线性相关关系,求y关于x的线性回归方程;
(2)根据统计每个城市汽车的盈利![]() (万元)与该城市4S店的个数x符合函数
(万元)与该城市4S店的个数x符合函数![]() ,
,![]() ,为扩大销售,该公司在同等规模的城市E预计要开设多少个4S店,才能使E市的4S店一个月某型号骑车销售盈利达到最大,并求出最大值.
,为扩大销售,该公司在同等规模的城市E预计要开设多少个4S店,才能使E市的4S店一个月某型号骑车销售盈利达到最大,并求出最大值.
附:回归方程![]() 中的斜率和截距的最小二乘法估计公式分别为:
中的斜率和截距的最小二乘法估计公式分别为: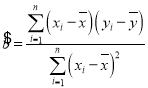 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运动员射击一次所得环数![]() 的分布如下:
的分布如下:
|
| 7 | 8 | 9 | 10 |
| 0 |
|
|
|
|
现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为![]() .
.
(Ⅰ)求该运动员两次都命中7环的概率.
(Ⅱ)求![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某文化创意公司开发出一种玩具(单位:套)进行生产和销售.根据以往经验,每月生产x套玩具的成本p由两部分费用(单位:元)构成:![]() .固定成本(与生产玩具套数x无关),总计一百万元;b.生产所需的直接总成本
.固定成本(与生产玩具套数x无关),总计一百万元;b.生产所需的直接总成本![]() .
.
(1)问:该公司每月生产玩具多少套时,可使得平均每套所需成本费用最少?此时每套玩具的成本费用是多少?
(2)假设每月生产出的玩具能全部售出,但随着x的增大,生产所需的直接总成本在急剧增加,因此售价也需随着x的增大而适当增加.设每套玩具的售价为q元,![]() (
(![]() ).若当产量为15000套时利润最大,此时每套售价为300元,试求
).若当产量为15000套时利润最大,此时每套售价为300元,试求![]() 、b的值.(利润=销售收入-成本费用)
、b的值.(利润=销售收入-成本费用)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com