
【题目】2019年9月1日,《西安市生活垃圾分类管理办法》正式实施.根据规定,生活垃圾分为可回收物、有害垃圾、厨余垃圾和其他垃圾,个人和单位如果不按规定进行垃圾分类将面临罚款,并纳入征信系统.为调查市民对垃圾分类的了解程度,某调查小组随机抽取了某小区的100位市民,请他们指出生活中若干项常见垃圾的种类,把能准确分类不少于3项的称为“比较了解”,少于三项的称为“不太了解”.调查结果如下:
0项 | 1项 | 2项 | 3项 | 4项 | 5项 | 5项以上 | |
男(人) | 1 | 5 | 15 | 8 | 6 | 7 | 3 |
女(人) | 0 | 4 | 11 | 13 | 10 | 12 | 5 |
(1)完成如下![]() 列联表并判断是否有99%的把握认为了解垃圾分类与性别有关?
列联表并判断是否有99%的把握认为了解垃圾分类与性别有关?
比较了解 | 不太了解 | 合计 | |
男 | |||
女 | |||
合计 |
(2)从对垃圾分类比较了解的市民中用分层抽样的方式抽取8位,现从这8位市民中随机选取两位,求至多有一位男市民的概率.
附: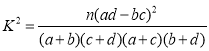
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,若椭圆经过点
,若椭圆经过点![]() ,且△PF1F2的面积为2.
,且△PF1F2的面积为2.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设斜率为1的直线![]() 与以原点为圆心,半径为
与以原点为圆心,半径为![]() 的圆交于A,B两点,与椭圆C交于C,D两点,且
的圆交于A,B两点,与椭圆C交于C,D两点,且![]() (
(![]() ),当
),当![]() 取得最小值时,求直线
取得最小值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系.直线
轴正半轴为极轴建立极坐标系.直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程与直线
的极坐标方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() 到其焦点下的距离为10.
到其焦点下的距离为10.
(1)求抛物线C的方程;
(2)设过焦点F的的直线![]() 与抛物线C交于
与抛物线C交于![]() 两点,且抛物线在
两点,且抛物线在![]() 两点处的切线分别交x轴于
两点处的切线分别交x轴于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且点
上,且点![]() 到点
到点![]() 的最大距离为
的最大距离为![]() ,点
,点![]() 到点
到点![]() 的最小距离为
的最小距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,坐标原点
两点,坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() (φ为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2是圆心为(2,
(φ为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2是圆心为(2,![]() ),半径为1的圆.
),半径为1的圆.
(1)求曲线C1的普通方程和C2的直角坐标方程;
(2)设M为曲线C1上的点,N为曲线C2上的点,求|MN|的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com