
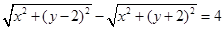 的点P(x,y)的轨迹是双曲线
的点P(x,y)的轨迹是双曲线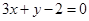 的距离等于到点P(1,-1)的距离的点的轨迹为抛物线
的距离等于到点P(1,-1)的距离的点的轨迹为抛物线| A.0 | B.1 | C.2 | D.3 |
科目:高中数学 来源:不详 题型:填空题
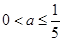 是
是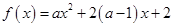 在区间
在区间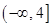 上为单调减函数的充要条件
上为单调减函数的充要条件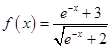 (e是自然对数的底数)的最小值为2.
(e是自然对数的底数)的最小值为2.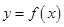 与它的反函数
与它的反函数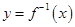 的图象若相交,则交点必在直线y="x" 上;
的图象若相交,则交点必在直线y="x" 上;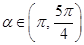 ,则
,则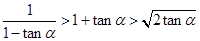 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
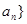 是等比数列,则数列{
是等比数列,则数列{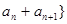 也是等比数列;
也是等比数列;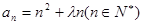 为单调递增数列,则
为单调递增数列,则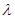 的取值范围是
的取值范围是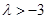 ;
;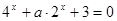 有实数解,则实数a的取值范围是
有实数解,则实数a的取值范围是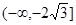 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
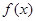 是定义在
是定义在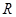 上的不恒为零的函数,且对任意
上的不恒为零的函数,且对任意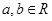 满足下列关系式:
满足下列关系式: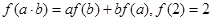 ,
,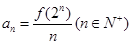 ,
,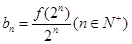 ,
,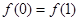 ; ②
; ②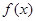 为偶函数; ③数列
为偶函数; ③数列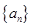 为等比数列;
为等比数列; 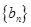 为等差数列。其中正确的结论是:_______。(将所有正确命题的序号都填上)
为等差数列。其中正确的结论是:_______。(将所有正确命题的序号都填上)查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
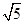 i,z2=
i,z2=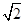 -
-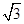 i,z3=-
i,z3=-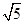 i,z4=2-i,那么这些复数的对应点共圆.
i,z4=2-i,那么这些复数的对应点共圆.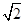 ,最小值为0.
,最小值为0.| A.0个 | B.1个 | C.2个 | D.3个 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
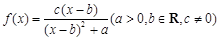 ,函数
,函数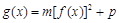 (
(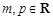 ,且mp<0),给出下列结论:
,且mp<0),给出下列结论: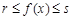 对于任意实数x恒成立;
对于任意实数x恒成立; 的图像关于点
的图像关于点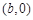 对称;
对称; 可能不存在零点(注:使关于x的方程
可能不存在零点(注:使关于x的方程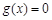 的实数x叫做函数
的实数x叫做函数 的零点);
的零点);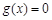 的解集可能为{-1,1,4,5}.
的解集可能为{-1,1,4,5}.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
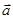 ,
, 的夹角为锐角”的充要条件是“
的夹角为锐角”的充要条件是“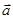 ·
· >0”;
>0”; )>
)>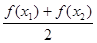 ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com