
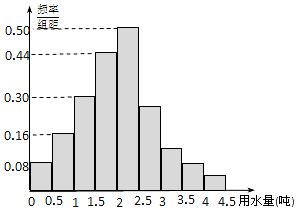
 某地区100位居民的人均月用水量(单位:t)的频率分布直方图及频数分布表如下:
某地区100位居民的人均月用水量(单位:t)的频率分布直方图及频数分布表如下:| 分组 | 频数 |
| [0,0.5) | 4 |
| [0.5,1) | 8 |
| [1,1.5) | 15 |
| [1.5,2) | 22 |
| [2,2.5) | 25 |
| [2.5,3) | 14 |
| [3,3.5) | 6 |
| [3.5,4) | 4 |
| [4,4.5) | 2 |
| 合计 | 100 |
分析 (1)频率最大的组的组中值,即为众数,累加各组组中与频率的乘积,可得平均数;
(2)累加月均用水量在3t以上的频率,进而得到月均用水量在3t以下的频率,可得结合.
解答 解:(1)由图知,这组数据的众数为2.25,
平均数
为0.25×0.04+0.75×0.08+1.25×0.15+1.75×0.22+2.25×0.25+2.75×0.14+3.25×0.06+3.75×0.04+4.25×0.02=2.02;
(2)人均月用水量在3t以上的居民的比例为6%+4%+2%=12%,
即大约是有12%的居民月均用水量在3t以上,
88%的居民月均用水量在3t以下,
因此,政府的解释是正确的.
点评 本题考查的知识点是频率分布直方图,频率分布直方表,难度不大,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x>y>z | B. | x>z>y | C. | y>x>z | D. | y>z>x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com