
【题目】如图1,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,以对角线
,以对角线![]() 为折痕把
为折痕把![]() 折起,使点
折起,使点![]() 到图2所示点
到图2所示点![]() 的位置,使得
的位置,使得![]() .
.
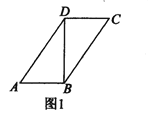

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)见解析; (Ⅱ)![]() .
.
【解析】
(Ⅰ)在图1中,求解三角形可得AB⊥BD,同理CD⊥BD,图2中,在△PAD中,求解三角形可得AD⊥PD,结合PD⊥BD,得到PD⊥平面ABD,进一步得到PD⊥AB,
又AB⊥BD,可得AB⊥平面PBD,由面面垂直的判定可得平面PAB⊥平面PBD;
(Ⅱ)以D为坐标原点,分别以DB,DP所在直线为y,z轴,过点D在平面ABD内平行于AB的直线为x轴建立空间直角坐标系,分别求出平面PAD与平面PAB的一个法向量,由两法向量所成角的余弦值可得二面角B-PA-D的余弦值.
(Ⅰ)图1中,![]() ,
,
由余弦定理得![]() ,
,
∴![]() ,∴
,∴![]() ,
,
即![]() ,
,
同理![]() .
.
图2中,在![]() 中,
中,![]() ,
,
∴![]() ,∴
,∴![]() ,即
,即![]()
又![]() ,∴
,∴![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,∴
,∴![]() ,
,
又![]() .∴
.∴![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(Ⅱ)如图,以![]() 为坐标原点,
为坐标原点,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,
过点![]() 在平面
在平面![]() 内平行于
内平行于![]() 的直线为
的直线为![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
则![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]()
由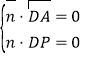 得
得![]() 令
令![]() ,得平面
,得平面![]() 的一个法向量为
的一个法向量为![]()
同理可得平面![]() 的一个法向量
的一个法向量![]()
∴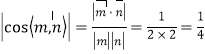 .
.
又二面角![]() 的平面角为锐角,
的平面角为锐角,
所以,二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 的一系列对应值如下表:
的一系列对应值如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据表格提供的数据求函数![]() 的一个解析式;
的一个解析式;
(2)根据(1)的结果,若函数![]() 周期为
周期为![]() ,当
,当![]() 时,方程
时,方程![]() 恰有两个不同的解,求实数
恰有两个不同的解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.回归直线![]() 至少经过其样本数据
至少经过其样本数据![]() 中的一个点
中的一个点
B.从独立性检验可知有99%的把握认为吃地沟油与患胃肠癌有关系时,我们就说如果某人吃地沟油,那么他有99%可能患胃肠癌
C.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
D.将一组数据的每一个数据都加上或减去同一个常数后,其方差也要加上或减去这个常数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线C1的极坐标方程是![]() ,在以极点为原点O,极轴为x轴正半轴(两坐标系取相同的单位长度)的直角坐标系xOy中,曲线C2的参数方程为
,在以极点为原点O,极轴为x轴正半轴(两坐标系取相同的单位长度)的直角坐标系xOy中,曲线C2的参数方程为![]() (θ为参数).
(θ为参数).
(1)求曲线C1的直角坐标方程与曲线C2的普通方程;
(2)将曲线C2经过伸缩变换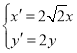 后得到曲线C3,若M,N分别是曲线C1和曲线C3上的动点,求|MN|的最小值.
后得到曲线C3,若M,N分别是曲线C1和曲线C3上的动点,求|MN|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某年级![]() 位同学参加语文和数学两门课的考试,每门课的考分从0到100分. 假如考试的结果没有两位同学的成绩是完全相同的(即至少有一门课的成绩不同). 另外,“甲比乙好”是指同学甲的语文和数学的考分均分别高于同学乙的语文和数学的考分. 试问:当
位同学参加语文和数学两门课的考试,每门课的考分从0到100分. 假如考试的结果没有两位同学的成绩是完全相同的(即至少有一门课的成绩不同). 另外,“甲比乙好”是指同学甲的语文和数学的考分均分别高于同学乙的语文和数学的考分. 试问:当![]() 最小为何值时,必存在三位同学(设为甲、乙、丙),有甲比乙好,乙比丙好.
最小为何值时,必存在三位同学(设为甲、乙、丙),有甲比乙好,乙比丙好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的焦距为8,其短轴的两个端点与长轴的一个端点构成正三角形。
的焦距为8,其短轴的两个端点与长轴的一个端点构成正三角形。
(1)求![]() 的方程;
的方程;
(2)设![]() 为
为![]() 的左焦点,
的左焦点,![]() 为直线
为直线![]() 上任意一点,过点
上任意一点,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于两点
于两点![]() ,
,![]() .
.
(i)证明:![]() 平分线段
平分线段![]() (其中
(其中![]() 为坐标原点);
为坐标原点);
(ii)当![]() 取最小值时,求点
取最小值时,求点![]() 的坐标。
的坐标。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣x2+ax,g(x)=ex﹣e,其中a>0.
(1)若a=1,证明:f(x)≤0;
(2)用max{m,n}表示m和n中的较大值,设函数h(x)=max{f(x),g(x)},讨论函数h(x)在(0,+∞)上的零点的个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com