
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
科目:高中数学 来源: 题型:解答题
 如图,在长方体OADB-CA1D1B1中,OA=3,OB=4,OC=2,OI=OJ=OK=1,点E,F分别是DB,D1B1的中点.设$\overrightarrow{OI}$=$\overrightarrow{i}$,$\overrightarrow{OJ}$=$\overrightarrow{j}$,$\overrightarrow{OK}$=$\overrightarrow{k}$,试用向量$\overrightarrow{i}$,$\overrightarrow{j}$,$\overrightarrow{k}$表示$\overrightarrow{O{D}_{1}}$、$\overrightarrow{O{A}_{1}}$、$\overrightarrow{OE}$、$\overrightarrow{OF}$.
如图,在长方体OADB-CA1D1B1中,OA=3,OB=4,OC=2,OI=OJ=OK=1,点E,F分别是DB,D1B1的中点.设$\overrightarrow{OI}$=$\overrightarrow{i}$,$\overrightarrow{OJ}$=$\overrightarrow{j}$,$\overrightarrow{OK}$=$\overrightarrow{k}$,试用向量$\overrightarrow{i}$,$\overrightarrow{j}$,$\overrightarrow{k}$表示$\overrightarrow{O{D}_{1}}$、$\overrightarrow{O{A}_{1}}$、$\overrightarrow{OE}$、$\overrightarrow{OF}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{3}$-y2=1 | B. | x2-$\frac{{y}^{2}}{3}$=1 | C. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{2}$=1 | D. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{3}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
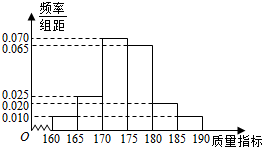 从某企业的一种产品中抽取40件产品,测量其某项质量指标,测量结果的频率分布直方图如图所示.
从某企业的一种产品中抽取40件产品,测量其某项质量指标,测量结果的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分类 人数(人) 时间 | 一小时以上 | 一小时以内 | 不使用 | 合计 |
| 上课时间 | 23 | 55 | m | 98 |
| 不上课时间 | 17 | 68 | 17 | 102 |
| 合计 | 40 | 123 | n | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com