
【题目】已知点P在曲线x2+y2=1上运动,过点P作x轴的垂线,垂足为Q,动点M满足![]() .
.
(1)求动点M的轨迹方程;
(2)点AB在直线x﹣y﹣4=0上,且AB=4,求△MAB的面积的最大值.
科目:高中数学 来源: 题型:
【题目】在棱长为1的正方体![]() 中,点
中,点![]() 是对角线
是对角线![]() 上的动点(点
上的动点(点![]() 与
与![]() 不重合),则下列结论正确的是__________.
不重合),则下列结论正确的是__________.
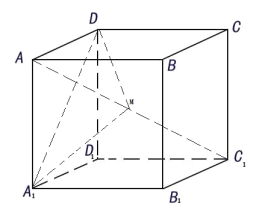
①存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
②存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
③若![]() 分别是
分别是![]() 在平面
在平面![]() 与平面
与平面![]() 的正投影的面积,则存在点
的正投影的面积,则存在点![]() ,使得
,使得![]() ;
;
④![]() 的面积可能等于
的面积可能等于![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十二生肖的座位次序如下图1,中间的狗、猪位置固定不动,其他生肖动物每次顺时针转动一格,即第一次转动后的座位次序如下图2,这样继续进行下去,那么第2019次换座位后,鼠的座位对应的编号为________.
图一:
鼠1 | 牛2 | 虎3 | 兔4 |
鸡10 | 狗11 | 猪12 | 龙5 |
猴9 | 羊8 | 马7 | 蛇6 |
图二:
鸡1 | 鼠2 | 牛3 | 虎4 |
猴10 | 狗11 | 猪12 | 兔5 |
羊9 | 马8 | 蛇7 | 龙6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在长方体ABCD﹣A1B1C1D1,若AB=BC,E,F分别是AB1,BC1的中点,则下列结论中不成立的是( )

A.EF与BB1垂直B.EF⊥平面BDD1B1
C.EF与C1D所成的角为45°D.EF∥平面A1B1C1D1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,近日我渔船编队在岛![]() 周围海域作业,在岛
周围海域作业,在岛![]() 的南偏西20°方向有一个海面观测站
的南偏西20°方向有一个海面观测站![]() ,某时刻观测站发现有不明船只向我渔船编队靠近,现测得与
,某时刻观测站发现有不明船只向我渔船编队靠近,现测得与![]() 相距31海里的
相距31海里的![]() 处有一艘海警船巡航,上级指示海警船沿北偏西40°方向,以40海里/小时的速度向岛
处有一艘海警船巡航,上级指示海警船沿北偏西40°方向,以40海里/小时的速度向岛![]() 直线航行以保护我渔船编队,30分钟后到达
直线航行以保护我渔船编队,30分钟后到达![]() 处,此时观测站测得
处,此时观测站测得![]() 间的距离为21海里.
间的距离为21海里.

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)试问海警船再向前航行多少分钟方可到岛![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过
,过![]() 且垂直于
且垂直于![]() 轴的焦点弦的弦长为
轴的焦点弦的弦长为![]() ,过
,过![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() ,
,![]() 互相垂直,直线
互相垂直,直线![]() 过
过![]() 且与椭圆
且与椭圆![]() 交于点
交于点![]() ,
,![]() 两点,直线
两点,直线![]() 过
过![]() 且与椭圆
且与椭圆![]() 交于
交于![]() ,
,![]() 两点.求
两点.求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,以棱长为1的正方体的三条棱所在直线为坐标轴,建立空间直角坐标系![]() ,点
,点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 上.
上.
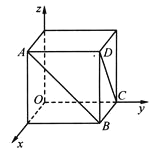
(1)当![]() ,且点
,且点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() 时,求
时,求![]() 的长度;
的长度;
(2)当点![]() 是面对角线
是面对角线![]() 的中点,点
的中点,点![]() 在面对角线
在面对角线![]() 上运动时,探究
上运动时,探究![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com