练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．已知f（x）=（x-a）（x-b）-2，（a＜b）的两个零点分别为α，β，（α＜β）则（　　）
    A．a＜α＜b＜βB．α＜a＜b＜βC．a＜α＜β＜bD．α＜a＜β＜b

    分析 可设g（x）=（x-a）（x-b），从而得到a，b是函数g（x）的两个零点，可看出f（x）的图象是由g（x）的图象向下平移2个单位得到，从而便可得出α＜a＜b＜β．

    解答 解：设g（x）=（x-a）（x-b），则a，b是g（x）的两个零点；
    函数f（x）的图象可以看成g（x）图象向下平移2个单位得到，且a＜b，α＜β，如图所示：

    ∴α＜a＜b＜β．
    故选B．

    点评 考查函数零点的概念，以及沿y轴方向的平移变换，要熟悉二次函数的图象．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

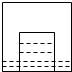    16．一天，小亮看到家中的塑料桶中有一个竖直放置的玻璃杯，桶子和玻璃杯的形状都是圆柱形，桶口的半径是杯口半径的2倍，其主视图如左图所示．小亮决定做个试验：把塑料桶和玻璃杯看作一个容器，对准杯口匀速注水，注水过程中杯子始终竖直放置，则下列能反映容器最高水位h与注水时间t之间关系的大致图象是（　　）
    A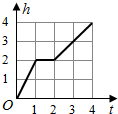．B．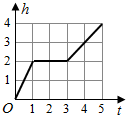
    C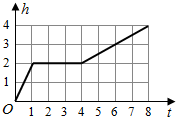．D．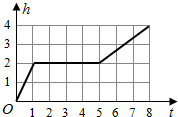

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．设f（x）=$\sqrt{x}$-alnx，a∈R
    （1）若a=2，求f（x）的最值；
    （2）若f（x）存在最小值，求其最小值g（a）的解析式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知$a+\frac{1}{a}=7$，则${a^{\frac{1}{2}}}+{a^{-\frac{1}{2}}}$=（　　）
    A．3B．9C．-3D．±3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．设函数$f（x）=\left\{\begin{array}{l}{3^x}，x≤0\\|{log_3}x|，x＞0\end{array}\right.$，则f（f（-1））的值为（　　）
    A．-1B．$\frac{1}{2}$C．1D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．（Ⅰ）计算0.0081${\;}^{\frac{1}{4}}$+（4${\;}^{-\frac{3}{4}}$）2+（$\sqrt{8}$）${\;}^{-\frac{4}{3}}$-16-0.75的值．
    （Ⅱ）计算lg25+lg2lg50+2${\;}^{1+lo{g}_{2}5}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．设命题p：x2+2x-3＜0 q：-5≤x＜1，则命题p成立是命题q成立的（　　）条件．
    A．充分不必要B．必要不充分
    C．充要D．既不充分也不必要

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知tanx=-1，且cosx=-$\frac{\sqrt{2}}{2}$，求x的取值集合．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．若函数f（x）=x+$\frac{1}{x-1}$（x＞1）在x=a处取最小值，则实数a=2．

    查看答案和解析>>

    同步练习册答案