
【题目】已知三棱柱ABC﹣A1B1C1的侧棱垂直于底面,∠BAC=90°,AB= AC = AA1=2,M,N分别是A1B1,BC的中点.

(1)证明:MN∥平面ACC1A1;
(2)求二面角M﹣AN﹣B的余弦值.
【答案】(1)见解析;(2)![]()
【解析】分析:(1)设AC的中点为D,连接DN,A1D,只要证明A1D∥MN,即可证明MN∥平面ACC1A1;(2)作出二面角M﹣AN﹣B的平面角,通过解三角形可求二面角M﹣AN﹣B的余弦值.
详解:
(1)证明:设AC的中点为D,连接DN,A1D
∵D,N分别是AC,BC的中点,∴![]()
又∵![]() ,
,
∴![]() ,∴四边形A1DNM是平行四边形
,∴四边形A1DNM是平行四边形
∴A1D∥MN
∵A1D平面ACC1A1,MN平面ACC1A1
∴MN∥平面ACC1A1
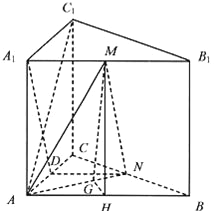
(2)如图,设AB的中点为H,连接MH,
∴MH∥BB1
∵BB1⊥底面ABC,∴MH⊥底面ABC
在平面ABC内,过点H做HG⊥AN,垂足为G
连接MG,∵AN⊥HG,AN⊥MH,HG∩MH=H
∴AN⊥平面MHG,则AN⊥MG
∴∠MGH是二面角M﹣AN﹣B的平面角
∵MH=BB1=2,
由AB=AC,∠BAN=45°,得HG=![]() ,所以
,所以![]()
所以cos∠MGH=![]() ∴二面角M﹣AN﹣B的余弦值是
∴二面角M﹣AN﹣B的余弦值是![]()


科目:高中数学 来源: 题型:
【题目】设p:实数x满足![]() ,其中a≠0,q:实数x满足
,其中a≠0,q:实数x满足![]() .
.
(I)若a=1,且p∧q为真,求实数x的取值范围.
(II)若p是q的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 满足
满足![]() ,且
,且![]() .
.
(![]() )求
)求![]() 的解析式.
的解析式.
(![]() )若函数
)若函数![]() 在区间
在区间![]() 上是单调函数,求实数
上是单调函数,求实数![]() 的取值范围.
的取值范围.
(![]() )若
)若![]() 关于的方程
关于的方程![]() 有区间
有区间![]() 上有唯一实数根,求实数
上有唯一实数根,求实数![]() 的取值范围(相等的实数根算一个).
的取值范围(相等的实数根算一个).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是平面,
是平面,![]() ,
,![]() 是直线,给出下列命题:
是直线,给出下列命题:
①若![]() ,
,![]() ,则
,则![]() ;
;
②若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
③如果![]() ,
,![]() ,
,![]() ,
,![]() 是异面直线,则
是异面直线,则![]() 与
与![]() 相交;
相交;
④若![]() .
.![]() ,且
,且![]() ,
,![]() ,则
,则![]() ,且
,且![]()
其中正确确命题的序号是_____(把正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015 年 12 月,华中地区数城市空气污染指数“爆表”,此轮污染为 2015 年以来最严重的污染过程,为了探究车流量与![]() 的浓度是否相关,现采集到华中某城市 2015 年 12 月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到华中某城市 2015 年 12 月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(提示数据:
的线性回归方程;(提示数据: ![]() )
)
(2)利用(1)所求的回归方程,预测该市车流量为 12 万辆时![]() 的浓度.
的浓度.
参考公式:回归直线的方程是![]() ,
,
其中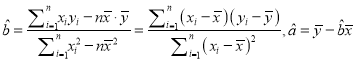 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是定义在
是定义在![]() 上的偶函数,
上的偶函数,![]() 的图象与
的图象与![]() 的图象关于直线
的图象关于直线![]() 对称,且当
对称,且当![]() 时,
时,![]() .
.
(![]() )求
)求![]() 的解析式.
的解析式.
(![]() )若
)若![]() 在
在![]() 上为增函数,求
上为增函数,求![]() 的取值范围.
的取值范围.
(![]() )是否存在正整数
)是否存在正整数![]() ,使
,使![]() 的图象的最高点落在直线
的图象的最高点落在直线![]() 上?若存在,求出
上?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com