
【题目】如图,在△ABC中,角A,B,C所对的边分别为a,b,c,且3bsinA=c,D为AC边上一点.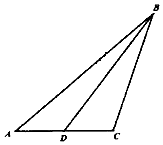
(1)若D是AC的中点,且 ![]() ,
, ![]() ,求△ABC的最短边的边长.
,求△ABC的最短边的边长.
(2)若c=2b=4,S△BCD= ![]() ,求DC的长.
,求DC的长.
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:高中数学 来源: 题型:
【题目】来自某校一班和二班的共计9名学生志愿服务者被随机平均分配到运送矿泉水、清扫卫生、维持秩序这三个岗位服务,且运送矿泉水岗位至少有一名一班志愿者的概率是 ![]() .
.
(1)求清扫卫生岗位恰好一班1人、二班2人的概率;
(2)设随机变量X为在维持秩序岗位服务的一班的志愿者的人数,求X分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,﹣ ![]() <φ<0)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0 , 2)和(x0+2π,﹣2).
<φ<0)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0 , 2)和(x0+2π,﹣2).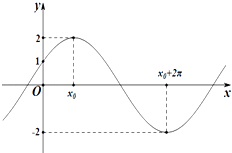
(1)求函数f(x)的解析式;
(2)若锐角θ满足f(2θ+ ![]() )=
)= ![]() ,求f(2θ)的值.
,求f(2θ)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数 ![]() (ω>0)的图象与x轴正半轴交点的横坐标构成一个公差为
(ω>0)的图象与x轴正半轴交点的横坐标构成一个公差为 ![]() 的等差数列,若要得到函数g(x)=Asinωx的图象,只要将f(x)的图象( )个单位.
的等差数列,若要得到函数g(x)=Asinωx的图象,只要将f(x)的图象( )个单位.
A.向左平移 ![]()
B.向右平移 ![]()
C.向左平移 ![]()
D.向右平移 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,圆C1:x2+y2=1经过伸缩变换 ![]() 后得到曲线C2以坐标原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线l的极坐标方程为cosθ+2sinθ=
后得到曲线C2以坐标原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线l的极坐标方程为cosθ+2sinθ= ![]()
(1)求曲线C2的直角坐标方程及直线l的直角坐标方程;
(2)在C2上求一点M,使点M到直线l的距离最小,并求出最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱台DEF﹣ABC中,AB=2DE,G,H分别为AC,BC的中点.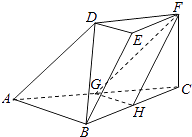
(Ⅰ)求证:BD∥平面FGH;
(Ⅱ)若CF⊥平面ABC,AB⊥BC,CF=DE,∠BAC=45°,求平面FGH与平面ACFD所成的角(锐角)的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一袋中有红、黄、蓝三种颜色的小球各一个,每次从中取出一个,记下颜色后放回,当三种颜色的球全部取出时停止取球,则恰好取5次球时停止取球的概率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.若a∈R,则“ ![]() <1”是“a>1”的必要不充分条件
<1”是“a>1”的必要不充分条件
B.“p∧q为真命题”是“p∨q为真命题”的必要不充分条件
C.若命题p:“x∈R,sinx+cosx≤ ![]() ”,则¬p是真命题
”,则¬p是真命题
D.命题“x0∈R,使得x02+2x0+3<0”的否定是“x∈R,x2+2x+3>0”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com