
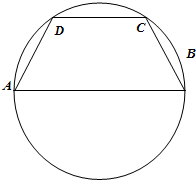
 已知线段AB的长为4,以AB为直径的圆有一内接梯形ABCD,其中AB∥CD(如图)则这个梯形的周长的最大值为( )
已知线段AB的长为4,以AB为直径的圆有一内接梯形ABCD,其中AB∥CD(如图)则这个梯形的周长的最大值为( )| A、8 | ||
| B、10 | ||
C、4(
| ||
| D、以上都不对 |
| π |
| 2 |
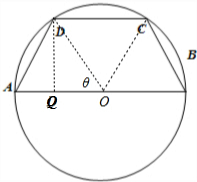
| QD2+AQ2 |
| θ |
| 2 |
| θ |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
| QD2+AQ2 |
| (2sinθ)2+(2-2cosθ)2 |
| 4sin2θ+4cos2θ-8cosθ+4 |
| 8-8cosθ |
8×2sin2
|
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| 1 |
| 2 |
| θ |
| 2 |
| 1 |
| 2 |
| π |
| 3 |


 每课必练系列答案
每课必练系列答案科目:高中数学 来源:2012年苏教版高中数学必修2 2.3空间直角坐标系练习卷(解析版) 题型:选择题
若已知A(1,1,1),B(-3,-3,-3),则线段AB的长为
A.4 B.2
B.2 C.4
C.4 D.3
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com