
【题目】某工厂对一批产品的质量进行了抽样检测,右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图.已知样本中产品净重在[70,75)克的个数是8个. 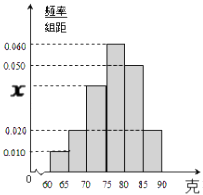
(Ⅰ)求样本容量;
(Ⅱ)若从净重在[60,70)克的产品中任意抽取2个,求抽出的2个产品恰好是净重在[65,70)的产品的概率.
【答案】解:设样本容量为N,由频率分布直方图可知:(0.01+0.02×2+x+0.05+0.06)×5=1 解得:x=0.04,
因为5x= ![]() ,解得N=40;
,解得N=40;
(Ⅱ)由频率分布直方图可知:
净重在[60,65)克的产品有0.01×5×40=2个;净重在[65,70)克的产品有0.02×5×40=4个;
所以净重在[60,70)克的产品有6个.
设净重在[60,65)克的产品编号为a,b;净重在[65,70)×克的4个产品编号为c,d,e,f
则从净重在[60,70)克的产品中任意抽取2个的所有基本事件有15种:
(a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e),(b,f),(a,b),(c,d),(c,e),(c,f),(d,e),(d,f),(e,f);
其中事件A“抽出的2个产品恰好是净重在[65,70)的产品”包含6个基本事件:
(c,d),(c,e),(c,f),(d,e),(d,f),(e,f);
所以由古典概型知p(A)= ![]()
【解析】(Ⅰ)频率分布直方图的所有正方形的面积和为1,即:(0.01+0.02×2+x+0.05+0.06)×5=1,求出x的值,再根据频率= ![]() 求解即可.量.(Ⅱ)这是一个古典概型,求出所有基本事件的个数,再求出“抽出的2个产品恰好是净重在[65,70)的产品”这个事件包含的基本事件的个数,再求概率即可.
求解即可.量.(Ⅱ)这是一个古典概型,求出所有基本事件的个数,再求出“抽出的2个产品恰好是净重在[65,70)的产品”这个事件包含的基本事件的个数,再求概率即可.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:高中数学 来源: 题型:
【题目】航空测量组的飞机航线和山顶在同一铅直平面内,已知飞机的高度为海拔10000m,速度为180km(千米)/h(小时),飞机先看到山顶的俯角为15°,经过420s(秒)后又看到山顶的俯角为45°,求山顶的海拔高度(取 ![]() ,
, ![]() ).
). 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,当∠xOy=α,且α∈(0, ![]() )∪(
)∪( ![]() ,π)时,定义平面坐标系xOy为α﹣仿射坐标系.在α﹣仿射坐标系中,任意一点P的斜坐标这样定义:
,π)时,定义平面坐标系xOy为α﹣仿射坐标系.在α﹣仿射坐标系中,任意一点P的斜坐标这样定义: ![]() 、
、 ![]() 分别为与x轴、y轴正向相同的单位向量,若
分别为与x轴、y轴正向相同的单位向量,若 ![]() =x
=x ![]() +y
+y ![]() ,则记为
,则记为 ![]() =(x,y).现给出以下说法:
=(x,y).现给出以下说法:
①在α﹣仿射坐标系中,已知 ![]() =(1,2),
=(1,2), ![]() =(3,t),若
=(3,t),若 ![]() ∥
∥ ![]() ,则t=6;
,则t=6;
②在α﹣仿射坐标系中,若 ![]() =(
=( ![]() ,
, ![]() ),若
),若 ![]() =(
=( ![]() ,﹣
,﹣ ![]() ),则
),则 ![]()
![]() =0;
=0;
③在60°﹣仿射坐标系中,若P(2,﹣1),则| ![]() |=
|= ![]() ;
;
其中说法正确的有 . (填出所有说法正确的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥P-ABC中,D为AB的中点。

(1)与BC平行的平面PDE交AC于点E,判断点E在AC上的位置并说明理由如下:
(2)若PA=PB,且△PCD为锐角三角形,又平面PCD⊥平面ABC,求证:AB⊥PC。
查看答案和解析>>
科目:高中数学 来源: 题型:
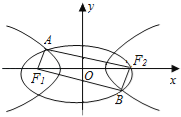
【题目】如图F1、F2是椭圆C1:![]() +y2=1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是( )
+y2=1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学同学的成绩如表:
n | 1 | 2 | 3 | 4 | 5 |
x0 | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同学的成绩x6及这6位同学成绩的标准差s;
(2)若从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间[68,75)中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用数学归纳法证明12+22+…+(n﹣1)2+n2+(n﹣1)2+…+22+12═ ![]() 时,由n=k的假设到证明n=k+1时,等式左边应添加的式子是( )
时,由n=k的假设到证明n=k+1时,等式左边应添加的式子是( )
A.(k+1)2+2k2
B.(k+1)2+k2
C.(k+1)2
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知PA垂直于矩形ABCD所在的平面,M,N分别是AB,PC的中点,若∠PDA=45°, 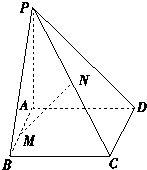
(1)求证:MN∥平面PAD且MN⊥平面PCD.
(2)探究矩形ABCD满足什么条件时,有PC⊥BD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com