
����Ŀ��ij���������ȡһ�꣨365�죩��100��Ŀ�������ָ��![]() �ļ�����������ͳ��������
�ļ�����������ͳ��������

��ij��ҵÿ���ɿ�����Ⱦ��ɵľ�����ʧ![]() ����λ��Ԫ������������ָ��
����λ��Ԫ������������ָ��![]() Ϊ
Ϊ![]() .��
.��![]() ʱ����ҵû����ɾ�����ʧ����
ʱ����ҵû����ɾ�����ʧ����![]() ����ҵ��ɾ�����ʧ��ֱ��ģ�ͣ���
����ҵ��ɾ�����ʧ��ֱ��ģ�ͣ���![]() ʱ��ɵľ�����ʧΪ
ʱ��ɵľ�����ʧΪ![]() ����
����![]() ʱ����ɵľ�����ʧ
ʱ����ɵľ�����ʧ![]() ����
����![]() ʱ��ɵľ�����ʧΪ2000Ԫ��
ʱ��ɵľ�����ʧΪ2000Ԫ��
��1����д��![]() �ı���ʽ��
�ı���ʽ��
��2���ڱ����������ȡһ�죬�Թ��Ƹ��쾭����ʧ����350Ԫ�ĸ��ʣ�
��3�������γ�ȡ������������30�����ڹ�ů����������12��Ϊ�ض���Ⱦ���������![]() �����������ж��ܷ���
�����������ж��ܷ���![]() �İ�����Ϊ���б�������ض���Ⱦ�빩ů�й���
�İ�����Ϊ���б�������ض���Ⱦ�빩ů�й���
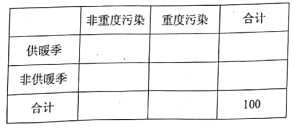
![]()
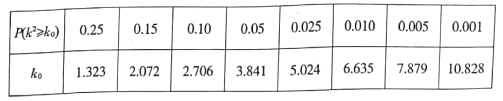
���𰸡�(1)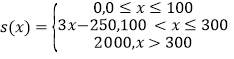 ��(2)0.38��(3)�𰸼�����.
��(2)0.38��(3)�𰸼�����.
��������
�����������1���ȸ��ݴ���ϵ������![]() ����ʽ�����÷ֶκ�����ʽд
����ʽ�����÷ֶκ�����ʽд![]() ����2������
����2������![]() ��
��![]() ����Ƶ�����ٸ���Ƶ�ʵ���Ƶ��������������ʣ���3���Ƚ����ݶ�Ӧ��������ݿ�����ʽ��
����Ƶ�����ٸ���Ƶ�ʵ���Ƶ��������������ʣ���3���Ƚ����ݶ�Ӧ��������ݿ�����ʽ��![]() �ο����ݱȽ����ж�.
�ο����ݱȽ����ж�.
�����������1��
��2���衰�ڱ����������ȡһ�죬���쾭����ʧ![]() ���ڳ���350Ԫ��Ϊ�¼�
���ڳ���350Ԫ��Ϊ�¼�![]() ������1��֪��
������1��֪��![]() ��Ƶ��Ϊ38����
��Ƶ��Ϊ38����![]() .
.
��3�������������ݵõ�����![]() ��������
��������

�����ɵ�![]()
![]()
������![]() �İ�����Ϊ���б�������ض���Ⱦ�빩ů�й�.
�İ�����Ϊ���б�������ض���Ⱦ�빩ů�й�.


 ��������ϵ�д�
��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��
��![]() ����
����
��������![]() ʱ������
ʱ������![]() �ĵ������䣮
�ĵ������䣮
����![]() ʱ��
ʱ��![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ҹ���ҽѧ�ķ�չ��ҩ�������ʹ����Ӧ��������.ÿ�괺ů�Ժ�������ǰ�������������뷱ֳ���ڣ����ڲɼ�����ҩ������.��֪һֻҩ������IJ�����![]() ��һ����Χ�ڵ��¶�
��һ����Χ�ڵ��¶�![]() �й������ǿ�����Ա��3�·ݵ�31���������ѡ��5������о������ռ��˸���ҩ�������5��۲��������±���
�й������ǿ�����Ա��3�·ݵ�31���������ѡ��5������о������ռ��˸���ҩ�������5��۲��������±���
���� | 2�� | 7�� | 15�� | 22�� | 30�� |
�¶� | 10 | 11 | 13 | 12 | 8 |
������ | 23 | 25 | 30 | 26 | 16 |
��1������5������ѡ2�죬��������ҩ������IJ��ѷֱ�Ϊ![]() ��
��![]() �����¼���
�����¼���![]() ��
��![]() ����С��25���ĸ��ʣ�
����С��25���ĸ��ʣ�
��2��������Աȷ�����о������ǣ��ȴ���������������ѡ2�飬��ʣ�µ�3�����ݽ���![]() ����
����![]() �����Իع鷽�����ٶԱ�ѡȡ��2�����ݽ��м���.
�����Իع鷽�����ٶԱ�ѡȡ��2�����ݽ��м���.
��������ѡȡ����3��2����30�յ��������ݣ������3��7�ա�15�պ�22������������ݣ����![]() ����
����![]() �����Իع鷽����
�����Իع鷽����
�������������Իع鷽�̵õ��Ĺ���������ѡ���ļ������ݵ�����������2��������Ϊ�õ������Իع鷽���ǿɿ��ģ����ʣ����������õ����Իع鷽���Ƿ�ɿ���
�����ع�ֱ�ߵ�б�ʺͽؾ����С���˹��ƹ�ʽ�ֱ�Ϊ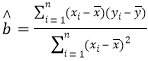 ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪{an}�ǵȲ����У�������{bn}��ǰn���ΪSn����2bn��b1��1+Sn����bn��0����a2b2��4��a7+b3��11��
��1����{an}��{bn}��ͨ�ʽ��
��2����cn��anbn��n��N*������{cn}��ǰn���Tn
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijͬѧ������㷨��������![]() ��ijһ�����ڵ�ͼ��ʱ���б��������˲������ݣ����±���
��ijһ�����ڵ�ͼ��ʱ���б��������˲������ݣ����±���
|
|
|
|
|
|
|
| �� |
| ||
|
|
|
|
|
|
��1���뽫��������Тٵ�������д�ڴ����Ӧλ���ϣ���ֱ��д������![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����������![]() ��ͼ�������е�ĺ������Ϊԭ����
��ͼ�������е�ĺ������Ϊԭ����![]() ���������겻�䣬�õ�����
���������겻�䣬�õ�����![]() ��ͼ����
��ͼ����![]() ʱ������
ʱ������![]() �ĵ����������䣻
�ĵ����������䣻
��3����������![]() ͼ���ϵ����е�����ƽ��
ͼ���ϵ����е�����ƽ��![]() ����λ���ȣ��õ�
����λ���ȣ��õ�![]() ��ͼ��. ��
��ͼ��. ��![]() ͼ���һ���Գ�����Ϊ
ͼ���һ���Գ�����Ϊ![]() ����
����![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�����
�У�����![]() �Ǿ��Σ�
�Ǿ��Σ�![]() ƽ��
ƽ��![]() ��
��![]() ����
����![]() ��
��![]() �ֱ����߶�
�ֱ����߶�![]() ��
��![]() �ϣ���
�ϣ���![]() ������
������![]() ������
������![]() ���ӳ�
���ӳ�![]() ��
��![]() ���ӳ��߽��ڵ�
���ӳ��߽��ڵ�![]() ������
������![]() ��
��

������֤��![]() ƽ��
ƽ��![]() ��
��
������![]() ʱ��������
ʱ��������![]() ������ֵ��
������ֵ��
������ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵΪ
���ɽǵ�����ֵΪ![]() ʱ����
ʱ����![]() ֵ��
ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]() ���ǵ����������У��������������е����С�����˳���ų�һ�У���ͬ������Ϊһ�����õ�һ��������
���ǵ����������У��������������е����С�����˳���ų�һ�У���ͬ������Ϊһ�����õ�һ��������![]() .
.
��1��������![]() ��
��![]() �ֱ�Ϊ�Ȳ�ȱ����У���
�ֱ�Ϊ�Ȳ�ȱ����У���![]() ��
�� ![]() ��
�� ![]() ����
����![]() ��
��
��2����![]() ������Ϊ1������Ϊ��������
������Ϊ1������Ϊ�������� ![]() ����������
����������![]() �ǵȲ����У�������
�ǵȲ����У�������![]() ��ǰ
��ǰ![]() ���
���![]() ��
��
��3����![]() ��
��![]() �Dz���2������������
�Dz�С��2������������![]() ���Ƿ���ڵȲ�����
���Ƿ���ڵȲ�����![]() ��ʹ�ö������
��ʹ�ö������![]() ����
����![]() ��
��![]() ֮������
֮������![]() ����������
����������![]() �������ڣ������һ����������ĵȲ�����
�������ڣ������һ����������ĵȲ�����![]() ���������ڣ���˵������.
���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������{an}��ǰn���ΪSn������![]() ��
��![]() .
.
��1��������{an}��ͨ�ʽ��
��2����![]() ����
����![]() �ǵ������У���ʵ��a��ȡֵ��Χ��
�ǵ������У���ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������ABC�У�AB��AC����BAC��90������AB��AC�ij��ֱ�Ϊ����x2��2��1![]() ��x+4
��x+4![]() 0������ʵ��������б��BC�������ڶ˵��E��F���㣬��EF��1����
0������ʵ��������б��BC�������ڶ˵��E��F���㣬��EF��1����![]() ��ȡֵ��ΧΪ_____��
��ȡֵ��ΧΪ_____��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com