
| A. | (-∞,0)∪(0,+∞) | B. | (0,+∞) | C. | (-∞,0)∪(3,+∞) | D. | (-∞,0) |
分析 构造函数g(x)=exf(x)-ex,(x∈R),研究g(x)的单调性,结合原函数的性质和函数值,解出即可.
解答 解:设g(x)=exf(x)-ex,(x∈R),
则g′(x)=exf(x)+exf′(x)-ex=ex[f(x)+f′(x)-1],
∵f′(x)+f(x>1,
∴f(x)+f′(x)-1>0,
∴g′(x)>0,
∴y=g(x)在定义域上单调递增,
∵exf(x)>ex+4,∴g(x)>4,
又∵g(0)=e0f(0)-e0=5-1=4,
∴g(x)>g(0),
∴x>0,
∴不等式的解集为(0,+∞)
故选:B.
点评 本题考查函数单调性与奇偶性的结合,结合已知条件构造函数,然后用导数判断函数的单调性是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
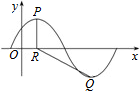 已知函数f(x)=Asin($\frac{π}{3}$x+φ),(A>0,0<φ<$\frac{π}{2}$),y=f(x)的部分图象如图所示,P,Q分别为该图象上相邻的最高点和最低点,点P在x轴上的射影为R(1,0),cos∠PRQ=-$\frac{4}{5}$
已知函数f(x)=Asin($\frac{π}{3}$x+φ),(A>0,0<φ<$\frac{π}{2}$),y=f(x)的部分图象如图所示,P,Q分别为该图象上相邻的最高点和最低点,点P在x轴上的射影为R(1,0),cos∠PRQ=-$\frac{4}{5}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有最大值62 | B. | 有最小值63 | C. | 有最大值62 | D. | 有最小值31 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数$f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<\frac{π}{2})$的部分图象如图所示.
已知函数$f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<\frac{π}{2})$的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com