
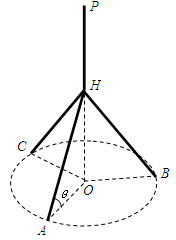
如图所示,某人想制造一个支架,它由四根金属杆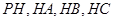 构成,其底端三点
构成,其底端三点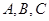 均匀地固定在半径为
均匀地固定在半径为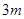 的圆
的圆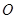 上(圆
上(圆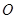 在地面上),
在地面上),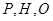 三点相异且共线,
三点相异且共线,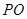 与地面垂直. 现要求点
与地面垂直. 现要求点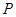 到地面的距离恰为
到地面的距离恰为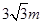 ,记用料总长为
,记用料总长为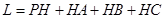 ,设
,设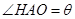 .
.
(1)试将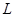 表示为
表示为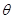 的函数,并注明定义域;
的函数,并注明定义域;
(2)当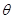 的正弦值是多少时,用料最省?
的正弦值是多少时,用料最省?
(1) ,
, ;(2)
;(2) .
.
解析试题分析:(1)由已知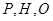 三点相异且共线,
三点相异且共线,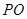 与地面垂直,且三点
与地面垂直,且三点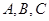 均匀地固定在半径为
均匀地固定在半径为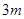 的圆
的圆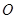 上,所以
上,所以 是全等的直角三角形,从而有
是全等的直角三角形,从而有 ,进而可得
,进而可得 ,再由点
,再由点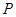 到地面的距离恰为
到地面的距离恰为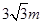 得
得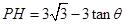 ;从而由
;从而由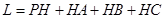 可将L表示为
可将L表示为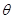 的函数;其定义域由图形可知:
的函数;其定义域由图形可知: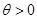 ,而当PH最短时角
,而当PH最短时角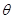 为最大,但由于
为最大,但由于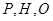 三点相异,所以
三点相异,所以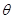 小于该最大值,从而求得其定义域;(2)用料最省,即L取得最小值;由(1)的函数利用导数方法来求使其取得最小值的
小于该最大值,从而求得其定义域;(2)用料最省,即L取得最小值;由(1)的函数利用导数方法来求使其取得最小值的 的值:先求出L的导函数,再令其等于零求出对应的
的值:先求出L的导函数,再令其等于零求出对应的 的值,再讨论函数的单调性就可确定
的值,再讨论函数的单调性就可确定 的值.
的值.
试题解析:(1)因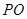 与地面垂直,且
与地面垂直,且 ,则
,则 是全等的直角三角形,又圆
是全等的直角三角形,又圆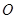 的半径为3,
的半径为3,
所以 ,
, , 3分
, 3分
又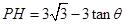 ,所以
,所以 , 6分
, 6分
若点 重合,则
重合,则 ,即
,即 ,所以
,所以 ,
,
从而 ,
, . 7分
. 7分
(2)由(1)知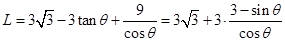 ,
,
所以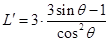 ,当
,当 时,
时, , 11分
, 11分
令 ,
, ,当
,当 时,
时, ;当
;当 时,
时, ;
;
所以函数L在 上单调递减,在
上单调递减,在 上单调递增, 15分
上单调递增, 15分
所以当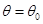 ,即
,即 时,L有最小值,此时用料最省. 16分
时,L有最小值,此时用料最省. 16分
考点:1.函数的应用;2.函数最值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
某通讯公司需要在三角形地带OAC区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域BOC内,乙中转站建在区域AOB内.分界线OB固定,且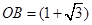 百米,边界线AC始终过点B,边界线OA、OC满足∠AOC=75°,∠AOB=30°,∠BOC=45°,设
百米,边界线AC始终过点B,边界线OA、OC满足∠AOC=75°,∠AOB=30°,∠BOC=45°,设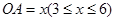 百米,
百米, 百米.
百米.
(1)试将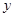 表示成
表示成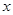 的函数,并求出函数
的函数,并求出函数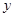 的解析式;
的解析式;
(2)当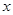 取何值时?整个中转站的占地面积
取何值时?整个中转站的占地面积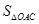 最小,并求出其面积的最小值.
最小,并求出其面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com