
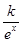 (e为自然对数的底数)万件,已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每件产品的售价x最低不低于35元,最高不超过41元.
(e为自然对数的底数)万件,已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每件产品的售价x最低不低于35元,最高不超过41元. 为常数
为常数 .
.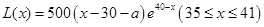 ;(Ⅱ)每件产品的售价为(31+a)元时,该产品一年的利润最大,最大利润为
;(Ⅱ)每件产品的售价为(31+a)元时,该产品一年的利润最大,最大利润为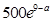 万元.
万元.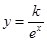 ,将每件产品的售价为40元时,该产品一年的销售量为500万件,代入可得k值,进而根据利润=单件利润×销售量得到该产品一年的利润L(x)万元与每件产品的售价x元的函数关系式;(Ⅱ)当每件产品的售价为多少元时,该产品一年的利润L(x)最大,由(Ⅰ)中所得函数的解析式,求导后分析函数的单调性,进而分析出该产品一年的利润L(x)的最大值.
,将每件产品的售价为40元时,该产品一年的销售量为500万件,代入可得k值,进而根据利润=单件利润×销售量得到该产品一年的利润L(x)万元与每件产品的售价x元的函数关系式;(Ⅱ)当每件产品的售价为多少元时,该产品一年的利润L(x)最大,由(Ⅰ)中所得函数的解析式,求导后分析函数的单调性,进而分析出该产品一年的利润L(x)的最大值.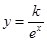 ,将
,将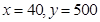 代入得
代入得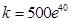 ,故该产品一年的销售量为
,故该产品一年的销售量为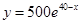 2分
2分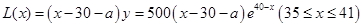 , 6分
, 6分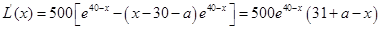 ,
,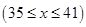
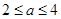 时,
时,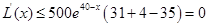 ,当且仅当
,当且仅当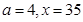 时取等号,故
时取等号,故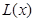 在
在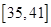 上单调递减,故
上单调递减,故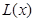 的最大值为
的最大值为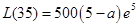 9分
9分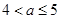 时,
时,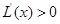 ?
?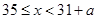 ,
,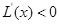 ?
?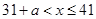 ,故
,故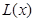 在
在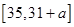 上单调递增,在
上单调递增,在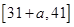 上单调递减,故
上单调递减,故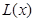 的最大值为
的最大值为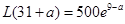 a12分综上所述,当
a12分综上所述,当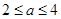 时,每件产品的售价为35元时,该产品一年的利润最大,最大利润为
时,每件产品的售价为35元时,该产品一年的利润最大,最大利润为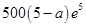 万元;当
万元;当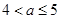 时,每件产品的售价为(31+a)元时,该产品一年的利润最大,最大利润为
时,每件产品的售价为(31+a)元时,该产品一年的利润最大,最大利润为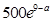 万元; 14分
万元; 14分

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源:不详 题型:解答题
 ,
, 为其反函数.
为其反函数. 与
与 图象的关系(只写出结论即可);
图象的关系(只写出结论即可); 的图象恒在
的图象恒在 的图象的上方;
的图象的上方;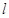 与
与 、
、 均相切,切点分别为(
均相切,切点分别为( )、(
)、( ),且
),且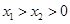 ,求证:
,求证: .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,高为
,高为 的等腰三角形及高为
的等腰三角形及高为 和
和 的两矩形所构成.设函数
的两矩形所构成.设函数 是图中阴影部分介于平行线
是图中阴影部分介于平行线 及
及 之间的那一部分的面积,则函数
之间的那一部分的面积,则函数 的图象大致为( )
的图象大致为( )


查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
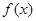 的定义域为
的定义域为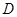 ,若满足:①
,若满足:①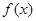 在
在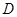 内是单调函数; ②存在
内是单调函数; ②存在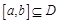
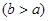 ,使得
,使得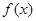 在
在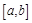 上的值域为
上的值域为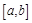 ,那么就称
,那么就称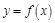 是定义域为
是定义域为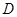 的“成功函数”.若函数
的“成功函数”.若函数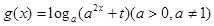 是定义域为
是定义域为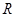 的“成功函数”,则
的“成功函数”,则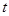 的取值范围为 ( )
的取值范围为 ( )A. | B. | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com