
【题目】已知长度为![]() 的线段
的线段![]() 的两个端点
的两个端点![]() 分别在
分别在![]() 轴和
轴和![]() 轴上运动,动点
轴上运动,动点![]() 满足
满足![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() ,且斜率不为零的直线
,且斜率不为零的直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,在
,在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得直线
,使得直线![]() 与
与![]() 的斜率之积为常数?若存在,求出定点
的斜率之积为常数?若存在,求出定点![]() 的坐标以及此常数;若不存在,请说明理由.
的坐标以及此常数;若不存在,请说明理由.
【答案】(1)![]() (2)存在两个定点
(2)存在两个定点![]() ,
,![]() ,使得直线
,使得直线![]() 与
与![]() 的斜率之积为常数,当定点为
的斜率之积为常数,当定点为![]() 时,常数为
时,常数为![]() ,当定点为
,当定点为![]() 时,常数为
时,常数为![]()
【解析】
(1)设![]() ,
,![]() ,
,![]() ,利用向量关系
,利用向量关系![]() 坐标化,可得曲线
坐标化,可得曲线![]() 的方程;
的方程;
(2)由题意设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() ,假设存在定点
,假设存在定点![]() ,使得直线
,使得直线![]() 与
与![]() 的斜率之积为常数,将
的斜率之积为常数,将![]() 表示成关于
表示成关于![]() 的函数,利用恒成立问题,可得定点坐标.
的函数,利用恒成立问题,可得定点坐标.
(1)设![]() ,
,![]() ,
,![]() ,
,
由于![]() ,所以
,所以![]() ,
,
即![]() ,所以
,所以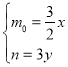 .又因为
.又因为![]() ,所以
,所以![]() ,
,
从而![]() ,即曲线
,即曲线![]() 的方程为
的方程为![]() .
.
(2)由题意设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() ,
,
由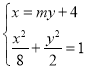 得
得![]() ,所以
,所以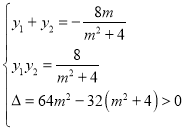 ,
,
故![]() ,
,![]() .
.
假设存在定点![]() ,使得直线
,使得直线![]() 与
与![]() 的斜率之积为常数,则
的斜率之积为常数,则
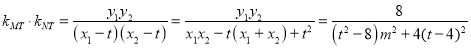 .
.
当![]() ,且
,且![]() 时,
时,![]() 为常数,解得
为常数,解得![]() .
.
显然当![]() 时,常数为
时,常数为![]() ;当
;当![]() 时,常数为
时,常数为![]() .
.
所以存在两个定点![]() ,
,![]() ,使得直线
,使得直线![]() 与
与![]() 的斜率之积为常数,当定点为
的斜率之积为常数,当定点为![]() 时,常数为
时,常数为![]() ,当定点为
,当定点为![]() 时,常数为
时,常数为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
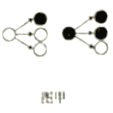
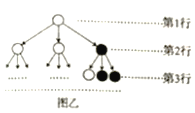
【题目】分形几何学是数学家伯努瓦·曼得尔布罗在20世纪70年代创立的一门新的数学学科,它的创立为解决传统科学众多领域的难题提供了全新的思路.按照如图甲所示的分形规律可得如图乙所示的一个树形图:记图乙中第![]() 行黑圈的个数为
行黑圈的个数为![]() ,则(1)
,则(1)![]() _______;(2)
_______;(2)![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学经典《数书九章》中,将底面为矩形且有一条侧棱与底面垂直的四棱锥称为“阳马”,将四个面都为直角三角形的四面体称之为“鳖臑”.在如图所示的阳马![]() 中,底面ABCD是矩形.
中,底面ABCD是矩形.![]() 平面
平面![]() ,
,![]() ,
,![]() ,以
,以![]() 的中点O为球心,AC为直径的球面交PD于M(异于点D),交PC于N(异于点C).
的中点O为球心,AC为直径的球面交PD于M(异于点D),交PC于N(异于点C).
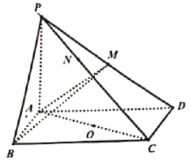
(1)证明:![]() 平面
平面![]() ,并判断四面体MCDA是否是鳖臑,若是,写出它每个面的直角(只需写出结论);若不是,请说明理由;
,并判断四面体MCDA是否是鳖臑,若是,写出它每个面的直角(只需写出结论);若不是,请说明理由;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市对所有高校学生进行普通话水平测试,发现成绩服从正态分布N(μ,σ2),下表用茎叶图列举出来抽样出的10名学生的成绩.
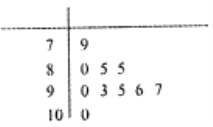
(1)计算这10名学生的成绩的均值和方差;
(2)给出正态分布的数据:P(μ﹣σ<X<μ+σ)=0.6826,P(μ﹣2σ<X<μ+2σ)=0.9544.
由(1)估计从全市随机抽取一名学生的成绩在(76,97)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】杨辉三角,是二项式系数在三角形中的一种几何排列.中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现了杨辉三角.在欧洲,帕斯卡在1654年也发现了这一规律,所以这个表又叫做帕斯卡三角形.杨辉三角是中国古代数学的杰出研究成果之一,它把二项式系数图形化,把组合数内在的一些代数性质直观地从图形中体现出来,是一种离散型的数与形的结合.
第0行 | 1 |
第1行 | 1 1 |
第2行 | 1 2 1 |
第3行 | 1 3 3 1 |
第4行 | 1 4 6 4 1 |
第5行 | 1 5 10 10 5 1 |
第6行 | 1 6 15 20 15 6 1 |
(1)记杨辉三角的前n行所有数之和为![]() ,求
,求![]() 的通项公式;
的通项公式;
(2)在杨辉三角中是否存在某一行,且该行中三个相邻的数之比为![]() ?若存在,试求出是第几行;若不存在,请说明理由;
?若存在,试求出是第几行;若不存在,请说明理由;
(3)已知n,r为正整数,且![]() .求证:任何四个相邻的组合数
.求证:任何四个相邻的组合数![]() ,
,![]() ,
,![]() ,
,![]() 不能构成等差数列.
不能构成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在R上的偶函数,且当
是定义在R上的偶函数,且当![]() 时,
时,![]() (
(![]() ).
).
(1)当![]() 时,求
时,求![]() 的表达式:
的表达式:
(2)求![]() 在区间
在区间![]() 的最大值
的最大值![]() 的表达式;
的表达式;
(3)当![]() 时,若关于x的方程
时,若关于x的方程![]() (a,
(a,![]() )恰有10个不同实数解,求a的取值范围.
)恰有10个不同实数解,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com