
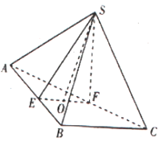
 如图,三棱锥S-ABC,E,F分别在线段AB,AC上,EF∥BC,△ABC,△SEF均是等边三角形,且平面SEF⊥平面ABC,若BC=4,EF=a,O为EF的中点.
如图,三棱锥S-ABC,E,F分别在线段AB,AC上,EF∥BC,△ABC,△SEF均是等边三角形,且平面SEF⊥平面ABC,若BC=4,EF=a,O为EF的中点.分析 (1)利用平面SEF⊥平面ABC,得出SO⊥平面ABC,BC⊥SO,
再由等边△ABC中AO⊥BC,得出BC⊥平面AOS,从而证明BC⊥AS;
(2)由SO⊥平面ABC得SO⊥BE,要使BE⊥平面SCD,则需BE⊥CO,
利用AE=EF求出a的值,得出此时BE⊥平面SCO.
解答 解:(1)证明:因为平面SEF⊥平面ABC,O为EF的中点,
且SE=SF,
∴SO⊥EF,
∴SO⊥平面ABC,
又BC?平面ABC,BC⊥SO,
而在等边△ABC中,AO⊥BC,
且SO∩AO=O,
∴BC⊥平面AOS,
又AS?平面AOS,∴BC⊥AS;
(2)平面SEF⊥平面ABC,O为EF的中点,且SE=SF,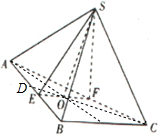
∴SO⊥平面ABC,故SO⊥BE,
要使BE⊥平面SCD,则需BE⊥CO,
延长CO交AB于D,则CD⊥AB,
DE=$\frac{1}{2}$EO=$\frac{1}{4}$a,
AD=2,
∴AE=2+$\frac{1}{4}$a,
即AE=EF
2+$\frac{1}{4}$a=a,
解得a=$\frac{8}{3}$;
∴a=$\frac{8}{3}$时,BE⊥平面SCO.
点评 本题考查了空间中的垂直关系的应用问题,是综合性题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,3,4} | B. | {1,3,4} | C. | {1,2,3,8,4,7} | D. | {0,1,2,3,4,7,8} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
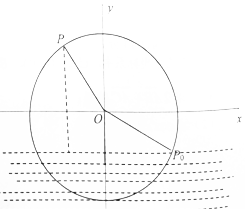 一半径为4米的水轮如图所示,水轮圆心O距离水面2米,已知水轮每60秒逆时针转动5圈,如果当水轮上点P从水中浮现时(图象P0点)开始计算时间,且点P距离水面的高度f(t)(米)与时间t(秒)满足函数:f(t)=Asin(ω+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$).
一半径为4米的水轮如图所示,水轮圆心O距离水面2米,已知水轮每60秒逆时针转动5圈,如果当水轮上点P从水中浮现时(图象P0点)开始计算时间,且点P距离水面的高度f(t)(米)与时间t(秒)满足函数:f(t)=Asin(ω+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com