
【题目】当前,以“立德树人”为目标的课程改革正在有序推进.高中联招对初三毕业学生进行体育测试,是激发学生、家长和学校积极开展体育活动,保证学生健康成长的有效措施.程度2019年初中毕业生升学体育考试规定,考生必须参加立定跳远、掷实心球、1分钟跳绳三项测试,三项考试满分50分,其中立定跳远15分,掷实心球15分,1分钟跳绳20分.某学校在初三上期开始时要掌握全年级学生每分钟跳绳的情况,随机抽取了100名学生进行测试,得到下边频率分布直方图,且规定计分规则如下表:
每分钟跳绳个数 |
|
|
|
|
得分 | 17 | 18 | 19 | 20 |
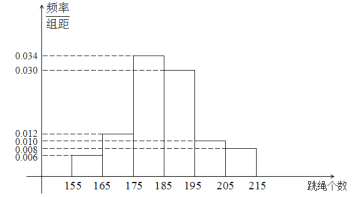
(Ⅰ)现从样本的100名学生中,任意选取2人,求两人得分之和不大于35分的概率;;
(Ⅱ)若该校初三年级所有学生的跳绳个数![]() 服从正态分布
服从正态分布![]() ,用样本数据的平均值和方差估计总体的期望和方差,已知样本方差
,用样本数据的平均值和方差估计总体的期望和方差,已知样本方差![]() (各组数据用中点值代替).根据往年经验,该校初三年级学生经过一年的训练,正式测试时每人每分钟跳绳个数都有明显进步,假设今年正式测试时每人每分钟跳绳个数比初三上学期开始时个数增加10个,现利用所得正态分布模型:
(各组数据用中点值代替).根据往年经验,该校初三年级学生经过一年的训练,正式测试时每人每分钟跳绳个数都有明显进步,假设今年正式测试时每人每分钟跳绳个数比初三上学期开始时个数增加10个,现利用所得正态分布模型:
![]() 预计全年级恰有2000名学生,正式测试每分钟跳182个以上的人数;(结果四舍五入到整数)
预计全年级恰有2000名学生,正式测试每分钟跳182个以上的人数;(结果四舍五入到整数)
![]() 若在全年级所有学生中任意选取3人,记正式测试时每分钟跳195以上的人数为ξ,求随机变量的分布列和期望.
若在全年级所有学生中任意选取3人,记正式测试时每分钟跳195以上的人数为ξ,求随机变量的分布列和期望.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
【答案】(I)![]() ;(II)
;(II)![]()
![]() ;
;![]() 详见解析.
详见解析.
【解析】
(Ⅰ)根据古典概率概率公式求解即可得到结果;(Ⅱ)先根据频率分布直方图得到平均数![]() 个,结合题意得到正式测试时
个,结合题意得到正式测试时![]() 根据正态曲线的对称性可得
根据正态曲线的对称性可得![]() ,由此可预计所求人数;
,由此可预计所求人数;![]() 由题意得
由题意得![]() ,根据独立重复试验的概率可得当
,根据独立重复试验的概率可得当![]() 分别取
分别取![]() 时的概率,然后可得分布列及期望.
时的概率,然后可得分布列及期望.
(Ⅰ)设“两人得分之和不大于35分”为事件A,则事件A包括两种情况:①两人得分均为17分;②两人中1人得17分,1人得18分.
由古典概型概率公式可得![]() ,
,
所以两人得分之和不大于35分的概率为![]() .
.
(Ⅱ)由频率分布直方图可得样本数据的平均数为
![]()
![]() (个),
(个),
又由![]() ,
,
所以正式测试时![]() ,
,
∴![]() .
.
![]() 由正态曲线的对称性可得
由正态曲线的对称性可得![]()
∴![]() (人),
(人),
所以可预计全年级恰有2000名学生,正式测试每分钟跳182个以上的人数为1683人.
![]() 由正态分布模型,全年级所有学生中任取1人,每分钟跳绳个数195以上的概率为0.5,
由正态分布模型,全年级所有学生中任取1人,每分钟跳绳个数195以上的概率为0.5,
所以![]()
∴![]()
![]()
![]()
![]() .
.
∴ ![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
∴![]() .
.


科目:高中数学 来源: 题型:
【题目】如图, ![]() 是边长为3的正方形,
是边长为3的正方形, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)在![]() 上是否存在一点
上是否存在一点![]() ,使平面
,使平面![]() 将几何体
将几何体![]() 分成上下两部分的体积比为
分成上下两部分的体积比为![]() ?若存在,求出点
?若存在,求出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:
质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
频数 | 6 | 26 | 38 | 22 | 8 |
(I)在答题卡上作出这些数据的频率分布直方图:
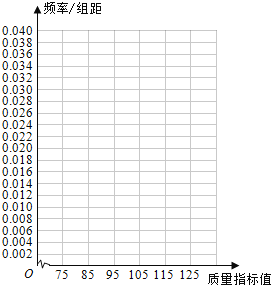
(II)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(III)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信抢红包”自2015年以来异常火爆,在某个微信群某次进行的抢红包活动中,若所发红包的总金额为8元,被随机分配为1.72元,1.83元,2.28元,1.55元,0.62元, 5份供甲、乙等5人抢,每人只能抢一次,则甲、乙二人抢到的金额之和不低于3元的概率是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司租地建仓库,每月土地占用费y1与仓库到车站的距离成反比,而每月库存货物的运费y2与到车站的距离成正比,如果在距离车站10km处建仓库,这两项费用y1和y2分别为2万元和8万元,那么要使这两项费用之和最小,仓库应建在距离车站( )
A.4kmB.5kmC.6kmD.7km
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com