
【题目】已知![]() 中,角
中,角![]() 所对的边分别是
所对的边分别是![]() ,
,![]() 的面积为
的面积为![]() ,且
,且![]() ,
,![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由已知利用三角形面积公式可得tanA=2,利用同角三角函数基本关系式可求sinA,cosA,由三角形内角和定理,两角和的余弦函数公式可求cosB的值.
(2)利用同角三角函数基本关系式可求sinB,利用正弦定理可得b的值,即可得S的值.
(1)∵S![]() bcsinA=bccosA,
bcsinA=bccosA,
∴sinA=2cosA,可得:tanA=2,
∵△ABC中,A为锐角,
又∵sin2A+cos2A=1,
∴可得:sinA![]() ,cosA
,cosA![]() ,
,
又∵C![]() ,
,
∴cosB=﹣cos(A+C)=﹣cosAcosC+sinAsinC![]() ,
,
(2)在△ABC中,sinB![]() ,
,
由正弦定理,可得:b![]() 3,
3,
∴S=bccosA=3.


科目:高中数学 来源: 题型:
【题目】运输公司![]() 年有
年有![]() 万辆公交车,计划
万辆公交车,计划![]() 年投入
年投入![]() 辆新型号公交车,以后每年投入的新型号公交车数量均比上年增加
辆新型号公交车,以后每年投入的新型号公交车数量均比上年增加![]() .
.
(1)![]() 年应投入多少辆新型号公交车?
年应投入多少辆新型号公交车?
(2)从![]() 年到
年到![]() 年间共投入多少辆新型号公交车?
年间共投入多少辆新型号公交车?
(3)从哪一年开始,该公司新型号公交车总量超过该公司公交车总量的![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的离心率为
)的离心率为![]() ,椭圆
,椭圆![]() 与
与![]() 轴交于
轴交于![]() 两点,且
两点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆![]() 上的一个动点,且点
上的一个动点,且点![]() 在
在![]() 轴的右侧,直线
轴的右侧,直线![]() 与直线
与直线![]() 交于
交于![]() 两点,若以
两点,若以![]() 为直径的圆与
为直径的圆与![]() 轴交于
轴交于![]() ,求点
,求点![]() 横坐标的取值范围及
横坐标的取值范围及![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且右焦点为
,且右焦点为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() .若
.若![]() ,求证:
,求证:![]() 为定值;
为定值;
(3)在(2)的条件下,若点![]() 不在椭圆
不在椭圆![]() 的内部,点
的内部,点![]() 是点
是点![]() 关于原点
关于原点![]() 的对称点,试求三角形
的对称点,试求三角形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将![]() 个不同的红球和
个不同的红球和![]() 个不同的白球,放入同一个袋中,现从中取出
个不同的白球,放入同一个袋中,现从中取出![]() 个球.
个球.
(1)若取出的红球的个数不少于白球的个数,则有多少种不同的取法;
(2)取出一个红球记![]() 分,取出一个白球记
分,取出一个白球记![]() 分,若取出
分,若取出![]() 个球的总分不少于
个球的总分不少于![]() 分,则有多少种不同的取法;
分,则有多少种不同的取法;
(3)若将取出的![]() 个球放入一箱子中,记“从箱子中任意取出
个球放入一箱子中,记“从箱子中任意取出![]() 个球,然后放回箱子中”为一次操作,如果操作三次,求恰有一次取到
个球,然后放回箱子中”为一次操作,如果操作三次,求恰有一次取到![]() 个红球并且恰有一次取到
个红球并且恰有一次取到![]() 个白球的概率.
个白球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲、乙两班各随机抽取10名同学,下面的茎叶图记录了这20名同学在2018年高考语文作文题目中的成绩(单位:分).已知语文作文题目满分为60分,“分数![]() 分,为及格;分数
分,为及格;分数![]() 分,为高分”,若甲、乙两班的成绩的平均分都是44分,
分,为高分”,若甲、乙两班的成绩的平均分都是44分,
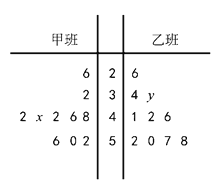
(1)求![]() 的值;
的值;
(2)若分别从甲、乙两班随机各抽取1名成绩为高分的学生,求抽到的学生中,甲班学生成绩高于乙班学生成绩的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com