
【题目】已知三棱锥![]() 如图
如图![]() 的展开图如图2,其中四边形ABCD为边长等于
的展开图如图2,其中四边形ABCD为边长等于![]() 的正方形,
的正方形,![]() 和
和![]() 均为正三角形.
均为正三角形.
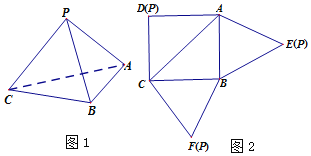
(1)证明:平面![]() 平面ABC;
平面ABC;
(2)若M是PC的中点,点N在线段PA上,且满足![]() ,求直线MN与平面PAB所成角的正弦值.
,求直线MN与平面PAB所成角的正弦值.
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() 、
、![]() 与平面
与平面![]() 所成的角依次是
所成的角依次是![]() 和
和![]() ,
,![]() ,
,![]() ,
,![]() 依次是
依次是![]() ,
,![]() 上的点,其中
上的点,其中![]() ,
,![]() .
.
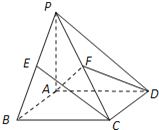
(1)求直线![]() 与平面
与平面![]() 所成的角(结果用反三角函数值表示);
所成的角(结果用反三角函数值表示);
(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某自来水公司要在公路两侧铺设水管,公路为东西方向,在路北侧沿直线铺设线路l1,在路南侧沿直线铺设线路l2,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB = 60m,BC = 80m,公路两侧铺设水管的费用为每米1万元,穿过公路的EF部分铺设水管的费用为每米2万元,设∠EFB= α,矩形区域内的铺设水管的总费用为W.
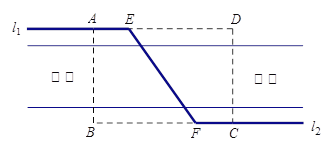
(1)求W关于α的函数关系式;
(2)求W的最小值及相应的角α.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是定义在
是定义在![]() 上的函数,若存在
上的函数,若存在![]() ,使得
,使得![]() 在
在![]() 单调递增,在
单调递增,在![]() 上单调递减,则称
上单调递减,则称![]() 为
为![]() 上的单峰函数,
上的单峰函数,![]() 为峰点,包含峰点的区间称为含峰区间,其含峰区间的长度为:
为峰点,包含峰点的区间称为含峰区间,其含峰区间的长度为:![]() .
.
(1)判断下列函数中,哪些是“![]() 上的单峰函数”?若是,指出峰点;若不是,说出原因;
上的单峰函数”?若是,指出峰点;若不是,说出原因;![]() ;
;
(2)若函数![]() 是
是![]() 上的单峰函数,求实数
上的单峰函数,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 是区间
是区间![]() 上的单峰函数,证明:对于任意的
上的单峰函数,证明:对于任意的![]() ,若
,若![]() ,则
,则![]() 为含峰区间;若
为含峰区间;若![]() ,则
,则![]() 为含峰区间;试问当
为含峰区间;试问当![]() 满足何种条件时,所确定的含峰区间的长度不大于0.6.
满足何种条件时,所确定的含峰区间的长度不大于0.6.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数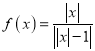 ,给出以下四个命题,其中真命题的序号是_______.
,给出以下四个命题,其中真命题的序号是_______.
①![]() 时,
时,![]() 单调递减且没有最值;
单调递减且没有最值;
②方程![]() 一定有解;
一定有解;
③如果方程![]() 有解,则解的个数一定是偶数;
有解,则解的个数一定是偶数;
④![]() 是偶函数且有最小值.
是偶函数且有最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
有时可用函数
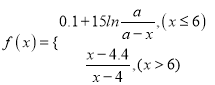
描述学习某学科知识的掌握程度,其中x表示某学科知识的学习次数(![]() ),
),![]() 表示对该学科知识的掌握程度,正实数a与学科知识有关.
表示对该学科知识的掌握程度,正实数a与学科知识有关.
(1) 证明:当![]() 时,掌握程度的增加量
时,掌握程度的增加量![]() 总是下降;
总是下降;
(2) 根据经验,学科甲、乙、丙对应的a的取值区间分别为![]() ,
,![]() ,
,
![]() .当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.
.当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com