Question

【题目】过抛物线y2=2px(p＞0)的焦点F的直线与抛物线相交于M、N两点，自M、N向准线l作垂线，垂足分别为M1、N1.

（1）求；

（2）记△FMM1、△FM1N1、△FNN1的面积分别为、、，求

Answer 1

【答案】（1）0；（2）4

【解析】

（1）先表示出F，的坐标，再向量坐标化，表示出的坐标，联立直线MN的方程和抛物线方程，根据韦达定理得到结果；（2）分别表示出面积表达式，S=4(p|－|)=4× (+)||· (+)·||[(+)2－4]=[+ (+)+ ]·||，联立直线和抛物线根据韦达定理得证即可.

.

（1）依题意，焦点为F(,0)，准线l的方程为x=－.

设点M，N的坐标分别为M(,)，N(,)，直线MN的方程为x=my+,则有M1(－,)，N1(－,)，=(－p,), =(－p,).

由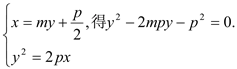

于是，+=2mp，=－.

∴·=+=－=0

（2）S=4成立，证明如下：

设M(,)，N(,)，

直线l与x轴的交点为，则由抛物线的定义得

|M M1|=|MF|=+, |N N1|=|NF|=+. 于是

=·|M M1|·| F1 M1|=(+)||，

=·| M1 N1|·|F F1|=p|－|，

=·|N N1|·| F1 N1|=(+)||，

∵S=4(p|－|)=4×(+)||·(+)·|| [(+)－4]=[+(+)+]·||.

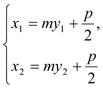将与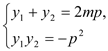代入上式化简可得 此式恒成立. 故=4.