
【题目】已知椭圆![]() 与直线
与直线![]() 有且只有一个交点,点P为椭圆C上任一点,
有且只有一个交点,点P为椭圆C上任一点,![]() ,
,![]() .若
.若![]() 的最小值为
的最小值为![]() .
.
(1)求椭圆C的标准方程;
(2)设直线![]() 与椭圆C交于不同两点A,B,点O为坐标原点,且
与椭圆C交于不同两点A,B,点O为坐标原点,且![]() ,当
,当![]() 的面积S最大时,求
的面积S最大时,求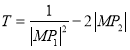 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)设点![]() ,利用向量的坐标运算研究
,利用向量的坐标运算研究![]() 的最小值,建立方程,求出
的最小值,建立方程,求出![]() 的值,即可得椭圆C的标准方程;
的值,即可得椭圆C的标准方程;
(2)设![]() ,
,![]() ,
,![]() ,将直线
,将直线![]() 与椭圆C联立,可得
与椭圆C联立,可得![]() 和
和![]() ,求出点O到直线l的距离,即可求出
,求出点O到直线l的距离,即可求出![]() 的面积S的表达式,利用基本不等式,求面积S的最大值,根据最大值的成立条件和前面求出的
的面积S的表达式,利用基本不等式,求面积S的最大值,根据最大值的成立条件和前面求出的![]() 和
和![]() ,可得点M的轨迹方程,进而可得
,可得点M的轨迹方程,进而可得![]() 的范围,将
的范围,将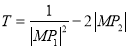 转化为
转化为![]() ,利用导数研究单调性即可求出
,利用导数研究单调性即可求出![]() 的取值范围.
的取值范围.
解:(1)设点![]() ,由题意知
,由题意知![]() ,
,![]() ,则
,则
![]() ,
,
当![]() 时,
时,![]() 取得最小值,即
取得最小值,即![]() ,
,
![]() ,
,![]() 故椭圆C的标准方程为
故椭圆C的标准方程为![]() ;
;
(2)设![]() ,
,![]() ,
,![]() ,则
,则
由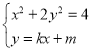 得
得![]() ,
,
![]() ,
,![]() ,
,
点O到直线l的距离![]() ,
,
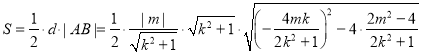
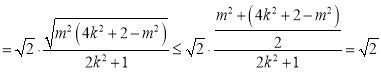 ,
,
S取得最大值![]() ,当且仅当
,当且仅当![]() 即
即![]() ,①
,①
此时![]() ,
,![]() ,
,
即![]() ,
,![]() 代入①式整理得,
代入①式整理得,![]() ,
,
即点M的轨迹为椭圆![]() ,
,
且点![]() ,
,![]() 为椭圆
为椭圆![]() 的左、右焦点,即
的左、右焦点,即![]() ,
,
记![]() ,则
,则![]() ,
,
从而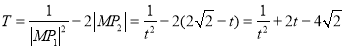 ,则
,则![]() ,
,
令![]() 可得
可得![]() ,即在T在
,即在T在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
且![]() ,
,![]() ,
,
故T的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系上,有一点列![]() ,设点
,设点![]() 的坐标
的坐标![]() (
(![]() ),其中
),其中![]() . 记
. 记![]() ,
,![]() ,且满足
,且满足![]() (
(![]() ).
).
(1)已知点![]() ,点
,点![]() 满足
满足![]() ,求
,求![]() 的坐标;
的坐标;
(2)已知点![]() ,
,![]() (
(![]() ),且
),且![]() (
(![]() )是递增数列,点
)是递增数列,点![]() 在直线
在直线![]() :
:![]() 上,求
上,求![]() ;
;
(3)若点![]() 的坐标为
的坐标为![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AD=2.
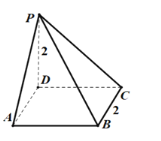
(1)求该四棱锥P-ABCD的表面积和体积;
(2)求该四棱锥P-ABCD内切球的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A是圆锥的顶点,![]() 是圆锥底面的直径,C是底面圆周上一点,
是圆锥底面的直径,C是底面圆周上一点,![]() ,
,![]() 与底面所成角的大小为60°,过点A作截面
与底面所成角的大小为60°,过点A作截面![]() ,截去部分后的几何体如图所示.
,截去部分后的几何体如图所示.
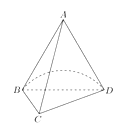
(1)求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(2)求该几何体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位共有老年人120人,中年人360人,青年人n人,为调查身体健康状况,需要从中抽取一个容量为m的样本,用分层抽样的方法进行抽样调查,样本中的中年人为6人,则n和m的值不可以是下列四个选项中的哪组( )
A.n=360,m=14B.n=420,m=15C.n=540,m=18D.n=660,m=19
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司在年终“尾牙”宴上对该公司年度的最佳销售员工进行奖励,已知员工![]() 一年以来的月销售业绩分别为:102,113,123,132,144,138,126,119,108,122,109,146.若该公司为最佳员工准备了相应的奖品,需要该员工通过抽奖游戏进行确定奖品金额,游戏规则如下:该员工需要从9张卡牌中不放回的抽取3张,其中1张卡牌的奖金为600元,4张卡牌的奖金均为400元,另外4张卡牌的奖金均为200元,所抽到的3张卡牌的金额之和
一年以来的月销售业绩分别为:102,113,123,132,144,138,126,119,108,122,109,146.若该公司为最佳员工准备了相应的奖品,需要该员工通过抽奖游戏进行确定奖品金额,游戏规则如下:该员工需要从9张卡牌中不放回的抽取3张,其中1张卡牌的奖金为600元,4张卡牌的奖金均为400元,另外4张卡牌的奖金均为200元,所抽到的3张卡牌的金额之和![]() 便是该员工所获得的奖品的最终价值.
便是该员工所获得的奖品的最终价值.
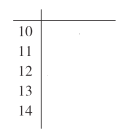
(Ⅰ)请根据题意完善员工![]() 的业绩的茎叶图,并求出员工
的业绩的茎叶图,并求出员工![]() 销售业绩的中位数;
销售业绩的中位数;
(Ⅱ)求![]() 的分布列以及数学期望.
的分布列以及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(1)求直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)若过![]() 且与直线
且与直线![]() 垂直的直线
垂直的直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 、
、![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com