练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知圆C：x2+y2+kx+2y+k2＝0，过点P（1，﹣1）可作圆的两条切线，则实数k的取值范围是_____．

    【答案】

    【解析】

    利用方程x2+y2+kx+2y+k2＝0表示一个圆可得：，解得：，再利过点P（1，﹣1）可作圆的两条切线可得：P（1，﹣1）在圆的外部，可得：12+（﹣1）2+k﹣2+k2＞0，解得：k＜﹣1或k＞0，问题得解。

    解：因为方程x2+y2+kx+2y+k2＝0表示一个圆，

    所以，解得：

    ∵过点P（1，﹣1）可作圆C：x2+y2+kx+2y+k2＝0的两条切线，

    ∴P（1，﹣1）在圆的外部，

    则12+（﹣1）2+k﹣2+k2＞0，

    即k2+k＞0，解得k＜﹣1或k＞0．

    由可得：或

    ∴实数k的取值范围是

    故答案为：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】命题p：f(x)＝－x2＋2ax＋1－a在x∈[0,1]时的最大值不超过2，命题q：正数x，y满足x＋2y＝8，且 恒成立. 若p∨(q)为假命题，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x2+ ，现有一组数据，绘制得到茎叶图，且茎叶图中的数据的平均数为2．（茎叶图中的数据均为小数，其中茎为整数部分，叶为小数部分）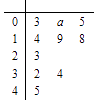
    （Ⅰ）求a的值；
    （Ⅱ）现从茎叶图小于3的数据中任取2个数据分别替换m的值，求恰有1个数据使得函数f（x）没有零点的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知△ABC和△A1B1C1满足sinA=cosA1 ， sinB=cosB1 ， sinC=cosC1 ．
    （1）求证：△ABC是钝角三角形，并求最大角的度数；
    （2）求sin2A+sin2B+sin2C的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知矩形ABCD与直角梯形ABEF，∠DAF=∠FAB=90°，点G为DF的中点，AF=EF= ，P在线段CD上运动．
    （1）证明：BF∥平面GAC；
    （2）当P运动到CD的中点位置时，PG与PB长度之和最小，求二面角P﹣CE﹣B的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设，数列{bn}满足：bn+1＝2bn+2，且an+1﹣an＝bn；

    （1）求证：数列{bn+2}是等比数列；

    （2）求数列{an}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设Sn为数列{an}的前n项和，已知，对任意n∈N*，都有2Sn＝（n+1）an．

    （1）求数列{an}的通项公式；

    （2）若数列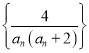的前项和为Tn，求Tn的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}的前n项和Sn= （an﹣1），数列{bn}满足bn+2=2bn+1﹣bn ， 且b6=a3 ， b60=a5 ， 其中n∈N*． （Ⅰ）求数列{an}，{bn}的通项公式；
    （Ⅱ）若cn=（﹣1）nbnbn+1 ， 求数列{cn}的前n项和Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的图象与函数的图象有三个不同的交点、、，其中．给出下列四个结论： ①；②；③；④．其中，正确结论的个数有（ ）个

    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    同步练习册答案