
【题目】某班主任为了对本班学生的月考成绩进行分析,从全班40名同学中随机抽取一个容量为6的样本进行分析.随机抽取6位同学的数学、物理分数对应如表:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 |
数学分数x | 60 | 70 | 80 | 85 | 90 | 95 |
物理分数y | 72 | 80 | 88 | 90 | 85 | 95 |
(1)根据上表数据用散点图说明物理成绩y与数学成绩x之间是否具有线性相关性?
(2)如果具有线性相关性,求出线性回归方程(系数精确到0.1);如果不具有线性相关性,请说明理由.
(3)如果班里的某位同学数学成绩为50,请预测这位同学的物理成绩。
![]() (附
(附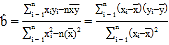 )
)
科目:高中数学 来源: 题型:
【题目】我国古代名著《庄子·天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思为:一尺的木棍,每天截取一半,永远都截不完.现将该木棍依此规律截取,如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度(单位:尺),则①②③处可分别填入的是


A. A B. B C. C D. D
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有6个完全相同的小球,分别标号为1,2,3,4,5,6.
(1)一次取出两个小球,求其号码之和能被3整除的概率;
(2)有放回的取球两次,每次取一个,求两个小球号码是相邻整数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系中![]() 轴的正半轴重合.若曲线
轴的正半轴重合.若曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将曲线![]() 的参数方程化为极坐标方程;
的参数方程化为极坐标方程;
(2)由直线![]() 上一点向曲线
上一点向曲线![]() 引切线,求切线长的最小值.
引切线,求切线长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】唐三彩,中国古代陶瓷烧制工艺的珍品,它吸取了中国国画、雕塑等工艺美术的特点,在中国文化中占有重要的历史地位,在陶瓷史上留下了浓墨重彩的一笔.唐三彩的生产至今已有1300多年的历史,制作工艺十分复杂,它的制作过程必须先后经过两次烧制,当第一次烧制合格后方可进入第二次烧制,两次烧制过程相互独立。某陶瓷厂准备仿制甲、乙、丙三件不同的唐三彩工艺品,根据该厂全面治污后的技术水平,经过第一次烧制后,甲、乙、丙三件工艺品合格的概率依次为![]() ,
, ![]() ,
, ![]() ,经过第二次烧制后,甲、乙、丙三件工艺品合格的概率依次为
,经过第二次烧制后,甲、乙、丙三件工艺品合格的概率依次为![]() ,
, ![]() ,
, ![]() .
.
(1)求第一次烧制后甲、乙、丙三件中恰有一件工艺品合格的概率;
(2)经过前后两次烧制后,甲、乙、丙三件工艺品成为合格工艺品的件数为![]() ,求随机变量
,求随机变量![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在空间中,下列命题正确的是
A.如果一个角的两边和另一角的两边分别平行,那么这两个角相等
B.两条异面直线所成的有的范围是![]()
C.如果两个平行平面同时与第三个平面相交,那么它们的交线平行
D.如果一条直线和平面内的一条直线平行,那么这条直线和这个平面平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,内角
中,内角![]() 、
、![]() 、
、![]() 所对的边分别是
所对的边分别是![]() 、
、![]() 、
、![]() ,不等式
,不等式![]() 对一切实数
对一切实数![]() 恒成立.
恒成立.
(1)求![]() 的取值范围;
的取值范围;
(2)当![]() 取最大值,且
取最大值,且![]() 的周长为
的周长为![]() 时,求
时,求![]() 面积的最大值,并指出面积取最大值时
面积的最大值,并指出面积取最大值时![]() 的形状.(参考知识:已知
的形状.(参考知识:已知![]() 、
、![]() ,
,![]() ;
;![]() 、
、![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com