
【题目】已知函数f(x)=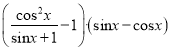 .
.
(l)求函数f(x)的定义域;
(2)求函数f(x)的值域.
【答案】(1){x∈R|x≠-![]() +2kπ,k∈Z}(2)
+2kπ,k∈Z}(2)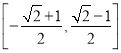
【解析】试题分析:(1)根据函数![]() 解析式,分母不为零,列出不等式求出解集即可求得函数
解析式,分母不为零,列出不等式求出解集即可求得函数![]() 的定义域;(2)利用二倍角的正弦公式、二倍角的余弦公式以及辅助角公式化简函数
的定义域;(2)利用二倍角的正弦公式、二倍角的余弦公式以及辅助角公式化简函数![]() 的解析式为一个角的三角函数形式,利用三角函数的有界性,即可求出
的解析式为一个角的三角函数形式,利用三角函数的有界性,即可求出![]() 的值域.
的值域.
试题解析:(1)由sinx+1≠0得,x≠-![]() +2kπ(k∈Z),
+2kπ(k∈Z),
∴f(x)的定义域为{x∈R|x≠![]() -+2kπ,k∈Z}.
-+2kπ,k∈Z}.
(2)f(x)=(![]() -1)(sinx-cosx)=(1-sinx-1)(sinx-cosx)
-1)(sinx-cosx)=(1-sinx-1)(sinx-cosx)
=-sinx(sinx-cosx)=sinxcosx-sin2x
=![]() sin2x-
sin2x-![]() = (sin2x+cos2x)
= (sin2x+cos2x) ![]()
=![]() sin(2x+
sin(2x+![]() )-
)-![]() {x|x≠-
{x|x≠-![]() +2kπ,k∈Z}
+2kπ,k∈Z}
虽然当x=-![]() +2kπ(k∈Z)时,f(x)=-1,但是
+2kπ(k∈Z)时,f(x)=-1,但是
f(x)=-1![]() {x|
{x| ![]() 或
或![]() ,k∈Z}
,k∈Z}![]() {x|x=-
{x|x=-![]() +2kπ,k∈Z}
+2kπ,k∈Z}
∴函数f(x)的值域为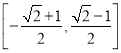


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,以椭圆长、短轴四个端点为顶点为四边形的面积为
,以椭圆长、短轴四个端点为顶点为四边形的面积为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
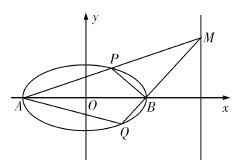
(Ⅱ)如图所示,记椭圆的左、右顶点分别为![]() 、
、![]() ,当动点
,当动点![]() 在定直线
在定直线![]() 上运动时,直线
上运动时,直线![]() 分别交椭圆于两点
分别交椭圆于两点![]() 、
、![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某体育场要建造一个长方形游泳池,其容积为4800m3 , 深为3m,如果建造池壁的单价为a且建造池底的单价是建造池壁的1.5倍,怎样设计水池的长和宽,才能使总造价最底?最低造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数![]() ,
, ![]() +1.
+1.
(1)若![]() ,曲线y=f(x)与
,曲线y=f(x)与![]() 在x=0处有相同的切线,求b;
在x=0处有相同的切线,求b;
(2)若![]() ,求函数
,求函数![]() 的单调递增区间;
的单调递增区间;
(3)若![]() 对任意
对任意![]() 恒成立,求b的取值区间
恒成立,求b的取值区间
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心为C的圆经过O(0,0))和A(4,0)两点,线段OA的垂直平分线和圆C交于M,N两点,且|MN|=2 ![]()
(1)求圆C的方程
(2)设点P在圆C上,试问使△POA的面积等于2的点P共有几个?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
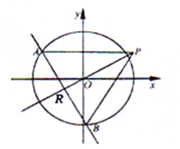
【题目】如图,椭圆![]() 的离心率为
的离心率为![]() ,其左焦点到点
,其左焦点到点![]() 的距离为
的距离为![]() .不过原点
.不过原点![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 两点,且线段
两点,且线段![]() 被直线
被直线![]() 平分.
平分.
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的面积取最大值时直线
的面积取最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
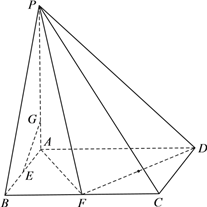
【题目】如图,四棱锥P-ABCD中,底面ABCD是矩形,PA![]() 面ABCD,且AB=2,AD=4,
面ABCD,且AB=2,AD=4,
AP=4,F是线段BC的中点.
⑴ 求证:面PAF![]() 面PDF;
面PDF;
⑵ 若E是线段AB的中点,在线段AP上是否存在一点G,使得EG![]() 面PDF?若存在,求出线段AG的长度;若不存在,说明理由.
面PDF?若存在,求出线段AG的长度;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于两个图形F1 , F2 , 我们将图象F1上任意一点与图形F2上的任意一点间的距离中的最小值,叫作图形F1与F2图形的距离,若两个函数图象的距离小于1,则这两个函数互为“可及函数”,给出下列几对函数,其中互为“可及函数”的是 . (写出所有正确命题的编号) ①f(x)=cosx,g(x)=2;
②f(x)=ex . g(x)=x;
③f(x)=log2(x2﹣2x+5),g(x)=sin ![]() ﹣x;
﹣x;
④f(x)=x+ ![]() ,g(x)=lnx+2.
,g(x)=lnx+2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com