
【题目】数学是研究数量、结构、变化、空间以及信息等概念的一门科学.在人类历史发展和社会生活中,数学发挥着不可替代的作用,也是学习和研究现代科学技术必不可少的基本工具.
(1)为调查大学生喜欢数学命题是否与性别有关,随机选取![]() 名大学生进行问卷调查,当被调查者问卷评分不低于
名大学生进行问卷调查,当被调查者问卷评分不低于![]() 分则认为其喜欢数学命题,当评分低于
分则认为其喜欢数学命题,当评分低于![]() 分则认为其不喜欢数学命题,问卷评分的茎叶图如下:
分则认为其不喜欢数学命题,问卷评分的茎叶图如下:
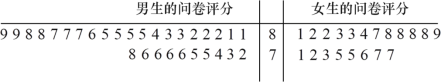
依据上述数据制成如下列联表:
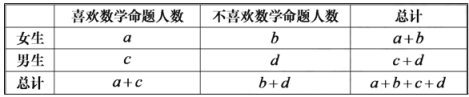
请问是否有![]() 的把握认为大学生是否喜欢数学命题与性别有关?
的把握认为大学生是否喜欢数学命题与性别有关?
参考公式及数据:![]() .
.
|
|
|
|
|
|
|
|
|
|
(2)在某次命题大赛中,![]() 同学要进行
同学要进行![]() 轮命题,其在每轮命题成功的概率均为
轮命题,其在每轮命题成功的概率均为![]() ,各轮命题相互独立,若该同学在
,各轮命题相互独立,若该同学在![]() 轮命题中恰有
轮命题中恰有![]() 次成功的概率为
次成功的概率为![]() ,记该同学在
,记该同学在![]() 轮命题中的成功次数为
轮命题中的成功次数为![]() ,求
,求![]() .
.
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的焦点分别为
的焦点分别为![]() 、
、![]() ,直线
,直线![]() :
:![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]()
(1)求椭圆的方程;
(2)过![]() 分别作互相垂直的两直线
分别作互相垂直的两直线![]() ,与椭圆分别交于D、E和M、N四点, 求四边形
,与椭圆分别交于D、E和M、N四点, 求四边形![]() 面积的最大值和最小值.
面积的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.若两条直线与同一条直线所成的角相等,则这两条直线平行
B.若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行
C.若一条直线分别平行于两个相交平面,则一定平行它们的交线
D.若两个平面都平行于同一条直线,则这两个平面平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对定义在[0,1]上,并且同时满足以下两个条件的函数f(x)称为G函数.
①对任意的x∈[0,1],总有f(x)≥0;
②当x1≥0,x2≥0,x1+x2≤1时,总有f(x1+x2)≥f(x1)+f(x2)成立.已知函数g(x)=x2与h(x)=2x﹣b是定义在[0,1]上的函数.
(1)试问函数g(x)是否为G函数?并说明理由;
(2)若函数h(x)是G函数,求实数b组成的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).M是曲线
为参数).M是曲线![]() 上的动点,将线段OM绕O点顺时针旋转
上的动点,将线段OM绕O点顺时针旋转![]() 得到线段ON,设点N的轨迹为曲线
得到线段ON,设点N的轨迹为曲线![]() .以坐标原点O为极点,
.以坐标原点O为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在(1)的条件下,若射线![]() 与曲线
与曲线![]() 分别交于A, B两点(除极点外),且有定点
分别交于A, B两点(除极点外),且有定点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】商家通常依据“乐观系数准则”确定商品销售价格,及根据商品的最低销售限价a,最高销售限价b(b>a)以及常数x(0<x<1)确定实际销售价格c=a+x(b﹣a),这里,x被称为乐观系数.
经验表明,最佳乐观系数x恰好使得(c﹣a)是(b﹣c)和(b﹣a)的等比中项,据此可得,最佳乐观系数x的值等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:
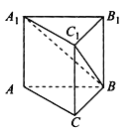
【题目】我国古代数学名著《九章算术》中有这样一些数学用语,“堑堵”意指底面为直角三角形,且侧棱垂直于底面的三棱柱,而“阳马”指底面为矩形且有一侧棱垂直于底面的四棱锥.现有一如图所示的堑堵,![]() ,若
,若![]() ,当阳马
,当阳马![]() 体积最大时,则堑堵
体积最大时,则堑堵![]() 的外接球的体积为________.
的外接球的体积为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别相交于点B、C,经过B、C两点的抛物线
轴分别相交于点B、C,经过B、C两点的抛物线![]() 与
与![]() 轴的另一交点为A,顶点为P,且对称轴为直线
轴的另一交点为A,顶点为P,且对称轴为直线![]() .
.
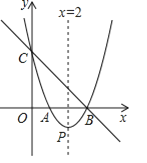
(1)求该抛物线的函数表达式;
(2)连结AC.请问在![]() 轴上是否存在点Q,使得以点P、B、Q为顶点的三角形与△ABC 相似,若存在,请求出点Q的坐标;若不存在,请说明理由.
轴上是否存在点Q,使得以点P、B、Q为顶点的三角形与△ABC 相似,若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com