
设f(x)=|x+1|+|x-3|.
(Ⅰ)解不等式f(x)≤3x+4;
(Ⅱ)若不等式f(x)≥m的解集为R,求实数m的取值范围.
(Ⅰ)不等式的解集为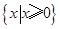 ;(Ⅱ)即
;(Ⅱ)即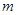 的取值范围为
的取值范围为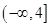 .
.
解析试题分析:(Ⅰ)解不等式f(x)≤3x+4,首先将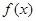 转化为分段函数
转化为分段函数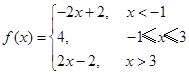 ,然后利用分段函数分段解不等式,从而求出不等式的解;易错点,不知将
,然后利用分段函数分段解不等式,从而求出不等式的解;易错点,不知将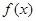 转化为分段函数;(Ⅱ)不等式
转化为分段函数;(Ⅱ)不等式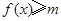 的解集为R,即当
的解集为R,即当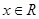 ,不等式
,不等式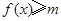 恒成立,只需求出
恒成立,只需求出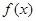 的最小值即可,此题可以利用分段函数求出最小值,也可利用绝对值不等式的性质来求最小值.
的最小值即可,此题可以利用分段函数求出最小值,也可利用绝对值不等式的性质来求最小值.
试题解析:(Ⅰ)因为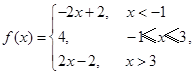 所以原不等式等价于
所以原不等式等价于
①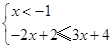 或②
或②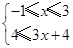 或③
或③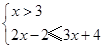 , 解得①无解,②
, 解得①无解,②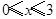 ,③
,③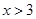 ,
,
因此不等式的解集为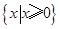 .
.
(Ⅱ)由于不等式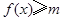 的解集为
的解集为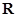 ,所以
,所以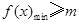 , 又
, 又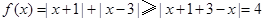 ,即
,即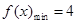 , 所以
, 所以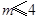 ,即
,即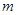 的取值范围为
的取值范围为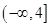 .
.
考点:绝对值不等式的解法,考查学生数形结合的能力以及化归与转化思想,以及学生的运算能力.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com