
分析 (Ⅰ)当a=1时,化简函数的解析式,去掉绝对值符号,即可求不等式f(x)<1的解集;
(Ⅱ)利用绝对值三角不等式推出f(x)的最大值为6的方程,即可求a的值.
解答 解:(Ⅰ)当a=1时,f(x)=|x+1|-|x-1|
当x<-1时,f(x)=-x-1+x-1=-2<1恒成立
当-1≤x≤1,f(x)=x+1+x-1=2x<1,$x<\frac{1}{2}$
当x>1,f(x)=x+1-x+1=2<1,无解
不等式f(x)=|x+1|-|x-1|<1的解集是$\left\{{x|x<\frac{1}{2}}\right\}$…(5分)
(Ⅱ)f(x)=|x+1|-|x-a|≤|(x+1)-(x-a)|=|1+a|
则|1+a|=6,所以a=5或a=-7…(10分)
点评 本题考查函数的最值的求法,绝对值不等式的解法,考查转化思想以及计算能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
 在某高校自主招生考试中,所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为A,B,C,D,E五个等级.某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为B的考生有10人.
在某高校自主招生考试中,所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为A,B,C,D,E五个等级.某考场考生的两科考试成绩数据统计如下图所示,其中“数学与逻辑”科目的成绩为B的考生有10人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
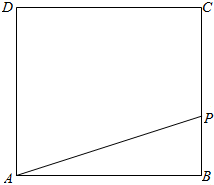 分别根据下列两个实际背景
分别根据下列两个实际背景查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,3) | B. | (2,4) | C. | (3,4] | D. | (2,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com